题目内容
已知,数列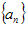 有
有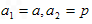 (常数
(常数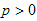 ),对任意的正整数
),对任意的正整数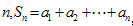 ,并有
,并有 满足
满足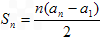 。
。
(1)求a的值;
(2)试确定数列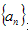 是不是等差数列,若是,求出其通项公式。若不是,说明理由;
是不是等差数列,若是,求出其通项公式。若不是,说明理由;
(3)令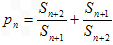 ,是否存在正整数M,使不等式
,是否存在正整数M,使不等式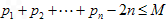 恒成立,若存在,求出M的最小值,若不存在,说明理由。
恒成立,若存在,求出M的最小值,若不存在,说明理由。
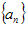 有
有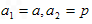 (常数
(常数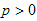 ),对任意的正整数
),对任意的正整数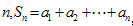 ,并有
,并有 满足
满足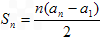 。
。(1)求a的值;
(2)试确定数列
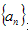 是不是等差数列,若是,求出其通项公式。若不是,说明理由;
是不是等差数列,若是,求出其通项公式。若不是,说明理由;(3)令
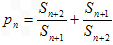 ,是否存在正整数M,使不等式
,是否存在正整数M,使不等式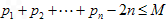 恒成立,若存在,求出M的最小值,若不存在,说明理由。
恒成立,若存在,求出M的最小值,若不存在,说明理由。解:(1)由已知,得 ,
,
∴a=0;
(2)由 得
得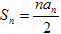 ,则
,则 ,
,
∴ ,即
,即 ,
,
于是有 ,并且有
,并且有 ,
,
∴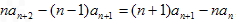 ,即
,即 ,
,
而n是正整数,则对任意 都有
都有 ,
,
∴数列 是等差数列,其通项公式是
是等差数列,其通项公式是 。
。
(3)∵ ,∴
,∴ ,
,
∴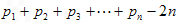 =
= =
= ;由n是正整数可得
;由n是正整数可得 ,
,
故存在最小的正整数M=3,使不等式 恒成立。
恒成立。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目