题目内容
如图所示，按棋盘格子形排列着16个点子，若从中每次选取不在一直线上的3个点，作为一个三角形的顶点，试问一共可作出多少个三角形？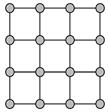
516
正面不好考虑，可考虑反面，
即选取3个点不能构成一个三角形顶点的情形，即三点共线的情形，反面情形可分为两类：（1)最多有4个点在同一直线上，有4行和4列和两对角线上的4点在同一直线上，如图（1），从这样的4点中选取三点的不同情形有
(4+4+2)×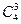
=40.
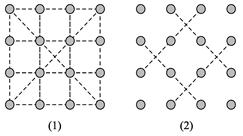
(2)最多有3个点在同一直线上，如图（2），只有4种不同情形.而从16个点中任取3个点有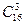
=560，减去不能构成三角形的上述二种情形，
∴不在同一直线的三点共有560-（40+4）=516（组），故共可作出516个三角形.
即选取3个点不能构成一个三角形顶点的情形，即三点共线的情形，反面情形可分为两类：（1)最多有4个点在同一直线上，有4行和4列和两对角线上的4点在同一直线上，如图（1），从这样的4点中选取三点的不同情形有
(4+4+2)×
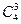=40.(2)最多有3个点在同一直线上，如图（2），只有4种不同情形.而从16个点中任取3个点有
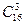=560，减去不能构成三角形的上述二种情形，∴不在同一直线的三点共有560-（40+4）=516（组），故共可作出516个三角形.
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
=_____________.
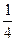
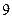个点，其中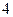
个点在一条直线上，此外无三点共线，连接这样的
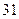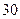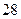条
条
条
条