题目内容
在北纬60°的纬线圈上有A、B两地,它们在纬度圈上所对应的劣弧长等于 (R为地球半径),则A、B两地的球面距离是 ( )
(R为地球半径),则A、B两地的球面距离是 ( )A.2R
B.R
C.
 R
RD.
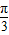 R
R
【答案】分析:先求出北纬60°圈所在圆的半径,是A、B两地在北纬60°圈上对应的圆心角,得到线段AB 的长,设地球的中心为O,解三角形求出∠AOB的大小,利用弧长公式求A、B这两地的球面距离.
解答:解:北纬60°圈所在圆的半径为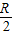 ,它们在纬度圈上所对应的劣弧长等于
,它们在纬度圈上所对应的劣弧长等于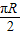 (R为地球半径),
(R为地球半径),
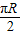 =θ×
=θ×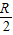 (θ是A、B两地在北纬60°圈上对应的圆心角),
(θ是A、B两地在北纬60°圈上对应的圆心角),
故 θ= ,∴线段AB=
,∴线段AB=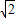 ×
×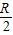 =
=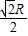 ,
,
设地球的中心为O,则△AOB中,由余弦定理得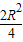 =R2+R2-2R2cos∠AOB,
=R2+R2-2R2cos∠AOB,
∴cos∠AOB= ,∠AOB=
,∠AOB=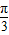 ,A、B这两地的球面距离是
,A、B这两地的球面距离是  ,
,
故选D.
点评:本题考查球的有关经纬度知识,球面距离,弧长公式,考查空间想象能力,逻辑思维能力,是基础题.
解答:解:北纬60°圈所在圆的半径为
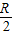 ,它们在纬度圈上所对应的劣弧长等于
,它们在纬度圈上所对应的劣弧长等于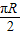 (R为地球半径),
(R为地球半径),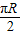 =θ×
=θ×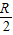 (θ是A、B两地在北纬60°圈上对应的圆心角),
(θ是A、B两地在北纬60°圈上对应的圆心角),故 θ=
 ,∴线段AB=
,∴线段AB=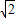 ×
×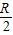 =
=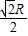 ,
,设地球的中心为O,则△AOB中,由余弦定理得
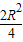 =R2+R2-2R2cos∠AOB,
=R2+R2-2R2cos∠AOB,∴cos∠AOB=
 ,∠AOB=
,∠AOB=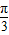 ,A、B这两地的球面距离是
,A、B这两地的球面距离是  ,
,故选D.
点评:本题考查球的有关经纬度知识,球面距离,弧长公式,考查空间想象能力,逻辑思维能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,(R为地球半径),则甲、乙两地的球面距离为( )
,(R为地球半径),则甲、乙两地的球面距离为( )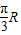



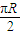 (R是地球的半径),则A,B两地的球面距离为 .
(R是地球的半径),则A,B两地的球面距离为 .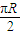 ,则这两地的球面距离是( )
,则这两地的球面距离是( )



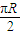 (R是地球的半径),则A,B两地的球面距离为 .
(R是地球的半径),则A,B两地的球面距离为 .