题目内容
已知球的半径为R,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?分析:由题意圆柱的底面为球的截面,由球的截面性质可得出圆柱的高为h、底面半径为r与球的半径为R的关系,再用h和r表示出圆柱的侧面积,利用基本不等式求最值即可.
解答: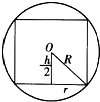 解:如图为轴截面,令圆柱的高为h,
解:如图为轴截面,令圆柱的高为h,
底面半径为r,侧面积为S,
则(
)2+r2=R2,
即h=2
.
∵S=2πrh=4πr•
=4π
≤4π
=2πR2,
取等号时,内接圆柱底面半径为
R,高为
R.
 解:如图为轴截面,令圆柱的高为h,
解:如图为轴截面,令圆柱的高为h,底面半径为r,侧面积为S,
则(
| h |
| 2 |
即h=2
| R2-r2 |
∵S=2πrh=4πr•
| R2-r2 |
=4π
| r2•(R2-r2) |
≤4π
|
取等号时,内接圆柱底面半径为
| ||
| 2 |
| 2 |
点评:本题考查球与圆柱的组合体问题、以及利用基本不等式求最值问题,难度一般.

练习册系列答案
相关题目
