题目内容
如图所示,椭圆C:![]() 的离心率
的离心率![]() ,左焦
,左焦
点为![]() 右焦点为
右焦点为![]() ,短轴两个端点为
,短轴两个端点为![]() .与
.与![]() 轴不垂直的直线
轴不垂直的直线![]() 与
与
椭圆C交于不同的两点![]() 、
、![]() ,记直线
,记直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)求证直线![]() 与
与![]() 轴相交于定点,并求出定点坐标.
轴相交于定点,并求出定点坐标.
(3)当弦![]() 的中点
的中点![]() 落在
落在![]() 内(包括边界)时,求直线
内(包括边界)时,求直线![]() 的斜率的取值。
的斜率的取值。
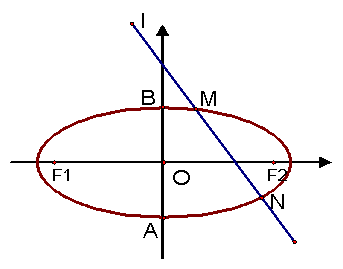
解:(1)由题意可知:椭圆C的离心率![]() ,
,![]()
![]()
故椭圆C的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,M、N坐标分别为
,M、N坐标分别为 ![]()
由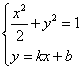 得
得![]()
∴![]()
∵![]() .
.
∴![]()
将韦达定理代入,并整理得![]() ,解得
,解得![]() .
.
∴直线![]() 与
与![]() 轴相交于定点(0,2)
轴相交于定点(0,2)
(3)由(2)中![]() ,其判别式
,其判别式![]() ,得
,得![]() .①
.①
设弦AB的中点P坐标为![]() ,则
,则![]() ,
,
![]() 弦
弦![]() 的中点
的中点![]() 落在
落在![]() 内(包括边界)
内(包括边界)
![]()

将坐标代入,整理得
解得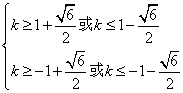 ②由①②得所求范围为
②由①②得所求范围为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,椭圆C:
如图所示,椭圆C: 如图所示,椭圆C:
如图所示,椭圆C: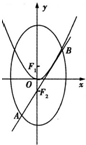 如图所示,椭圆C:
如图所示,椭圆C: 如图所示,椭圆C:
如图所示,椭圆C: (2010•茂名二模)如图所示,椭圆
(2010•茂名二模)如图所示,椭圆