题目内容
已知二次函数f(x)=ax2+bx+c(a>0)的图象与x轴有两个不同的公共点,若f(c)=0且0<x<c时,f(x)>0.(1)试比较
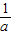 与c的大小;
与c的大小;(2)证明:-2<b<-1.
【答案】分析:(1)由题意得c、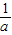 是方程f(x)=0的两个根,欲比较
是方程f(x)=0的两个根,欲比较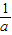 与c的大小,利用反证法去证明
与c的大小,利用反证法去证明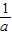 <c不可能,从而得到
<c不可能,从而得到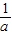 >c;
>c;
(2)先由f(c)=0,得b=-1-ac.从而得到b<-1,再利用(1)的结论,比较f(x)图象的对称轴与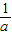 的大小,从而确定b的取值范围即可.
的大小,从而确定b的取值范围即可.
解答:解:(1)∵f(x)的图象与x轴有两个不同的交点,
∴f(x)=0有两个不同的实数根x1,x2.
∵f(c)=0,
∴c是方程f(x)=0的一个根,
不妨设x1=c,
∵x1x2=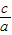 ,∴x2=
,∴x2=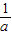 (
(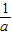 ≠c),
≠c),
假设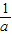 <c,又
<c,又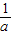 >0,由0<x<c时,f(x)>0,
>0,由0<x<c时,f(x)>0,
得f(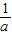 )>0,与已知f(
)>0,与已知f(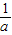 )=0矛盾,∴
)=0矛盾,∴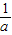 >c.
>c.
(2)证明:由f(c)=0,得ac+b+1=0,
∴b=-1-ac.
又a>0,c>0,∴b<-1.
f(x)图象的对称轴方程为
x=-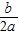 =
= =
=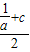 <
<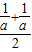 =
= ,
,
即-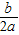 <
<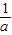 .
.
又a>0,∴b>-2,∴-2<b<-1.
点评:本题主要考查不等式的证明,有些不等式无法利用用题设的已知条件直接证明,我们可以间接的方法--反证法去证明,
即通过否定原结论---导出矛盾---从而达到肯定原结论的目的.
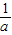 是方程f(x)=0的两个根,欲比较
是方程f(x)=0的两个根,欲比较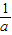 与c的大小,利用反证法去证明
与c的大小,利用反证法去证明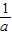 <c不可能,从而得到
<c不可能,从而得到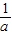 >c;
>c;(2)先由f(c)=0,得b=-1-ac.从而得到b<-1,再利用(1)的结论,比较f(x)图象的对称轴与
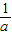 的大小,从而确定b的取值范围即可.
的大小,从而确定b的取值范围即可.解答:解:(1)∵f(x)的图象与x轴有两个不同的交点,
∴f(x)=0有两个不同的实数根x1,x2.
∵f(c)=0,
∴c是方程f(x)=0的一个根,
不妨设x1=c,
∵x1x2=
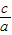 ,∴x2=
,∴x2=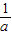 (
(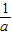 ≠c),
≠c),假设
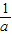 <c,又
<c,又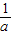 >0,由0<x<c时,f(x)>0,
>0,由0<x<c时,f(x)>0,得f(
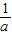 )>0,与已知f(
)>0,与已知f(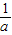 )=0矛盾,∴
)=0矛盾,∴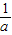 >c.
>c.(2)证明:由f(c)=0,得ac+b+1=0,
∴b=-1-ac.
又a>0,c>0,∴b<-1.
f(x)图象的对称轴方程为
x=-
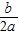 =
= =
=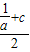 <
<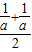 =
= ,
,即-
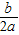 <
<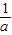 .
.又a>0,∴b>-2,∴-2<b<-1.
点评:本题主要考查不等式的证明,有些不等式无法利用用题设的已知条件直接证明,我们可以间接的方法--反证法去证明,
即通过否定原结论---导出矛盾---从而达到肯定原结论的目的.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目