题目内容
已知| |=1,|
|=1,| |=2,∠AOB=
|=2,∠AOB= ,
, ,且x+2y=1,则|
,且x+2y=1,则| |的最小值为________.
|的最小值为________.

分析:利用向量的数量积和二次函数的性质即可得出.
解答:∵|
 |=1,|
|=1,| |=2,∠AOB=
|=2,∠AOB= ,
, ,且x+2y=1,
,且x+2y=1,∴
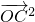 =
=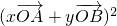 =x2+4y2
=x2+4y2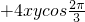 =x2+4y2-2xy=(1-2y)2+4y2-2y(1-2y)
=x2+4y2-2xy=(1-2y)2+4y2-2y(1-2y)=12y2-6y+1=
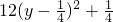
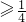 ,当且仅当
,当且仅当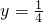 ,x=
,x= 时取等号.
时取等号.∴
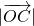
 .
.故|
 |的最小值为
|的最小值为 .
.故答案为
 .
.点评:熟练掌握向量的数量积运算性质和二次函数的性质是解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
已知
(xcosx+3a-b)dx=2a+6,f(t)=
(x3+ax+5a-b)dx为偶函数,则a+b=( )
| ∫ | 1 -1 |
| ∫ | t 0 |
| A、-6 | B、-12 | C、4 | D、-4 |