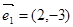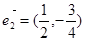题目内容
下列向量组中,能作为表示它们所在平面内所有向量的基底的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
分析:可以作为基底的向量需要是不共线的向量,可以从向量的坐标发现A,B,D选项中的两个向量均共线,得到正确结果是C.
解答:解:可以作为基底的向量需要是不共线的向量,
A中一个向量是零向量,两个向量共线,不合要求
B中两个向量是
=
,两个向量共线,
D项中的两个向量也共线,
故选C.
A中一个向量是零向量,两个向量共线,不合要求
B中两个向量是
| e 1 |
| 1 |
| 2 |
| e 2 |
D项中的两个向量也共线,
故选C.
点评:由于向量有几何法和坐标法两种表示方法,所以我们应根据题目的特点去选择向量的表示方法,由于坐标运算方便,可操作性强,因此应优先选用向量的坐标运算.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
下列向量组中,能作为表示它们所在平面内所有向量的基底的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在下列向量组中,能作为表示它们所在平面内所有向量的基底的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
下列向量组中,能作为平面内所有向量基底的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
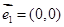
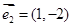 B.
B.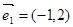
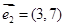
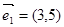
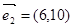 D.
D.