题目内容
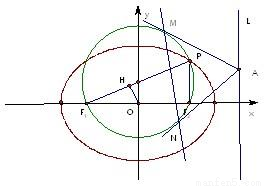
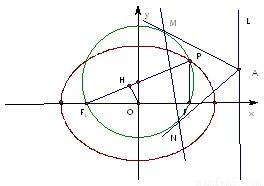
已知椭圆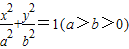 左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,
左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,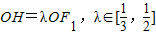 .
.(1)求椭圆的离心率e的取值范围;
(2)当e取最大值时,过F1,F2,P的圆Q的截y轴的线段长为6,求圆Q的方程;
(3)在(2)的条件下,过椭圆右准线L上任一点A引圆Q的两条切线,切点分别为M,N,试探究直线MN是否过定点?若过定点,请求出该定点;否则,请说明理由.
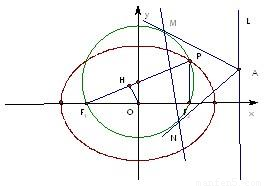
【答案】分析:由相似三角形知,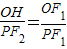 ,
,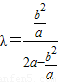 ,2a2λ-b2λ=b2,2a2λ=b2(1+λ),
,2a2λ-b2λ=b2,2a2λ=b2(1+λ),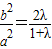 .
.
(1)由 ,知
,知 ,在
,在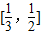 上单调递减.由此能求出椭圆的离心率e的取值范围.
上单调递减.由此能求出椭圆的离心率e的取值范围.
(2)当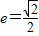 时,
时,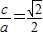 ,所以
,所以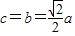 ,2b2=a2.由PF2⊥F1F2,知PF1是圆的直径,圆心是PF1的中点,由此能求出圆Q的方程.
,2b2=a2.由PF2⊥F1F2,知PF1是圆的直径,圆心是PF1的中点,由此能求出圆Q的方程.
(3)椭圆方程是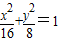 ,右准线方程为
,右准线方程为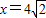 ,由直线AM,AN是圆Q的两条切线,知切点M,N在以AQ为直径的圆上.设A点坐标为
,由直线AM,AN是圆Q的两条切线,知切点M,N在以AQ为直径的圆上.设A点坐标为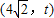 ,由此能够导出直线MN必过定点
,由此能够导出直线MN必过定点 .
.
解答:解:由相似三角形知,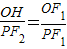 ,
,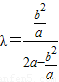 ,
,
∴2a2λ-b2λ=b2,2a2λ=b2(1+λ),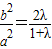 .
.
(1) ,∴
,∴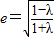 ,在
,在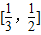 上单调递减.
上单调递减.
∴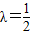 时,e2最小
时,e2最小 ,
,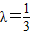 时,e2最大
时,e2最大 ,
,
∴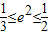 ,∴
,∴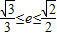 .
.
(2)当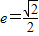 时,
时,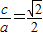 ,∴
,∴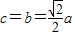 ,∴2b2=a2.
,∴2b2=a2.
∵PF2⊥F1F2,∴PF1是圆的直径,圆心是PF1的中点,
∴在y轴上截得的弦长就是直径,∴PF1=6.
又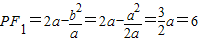 ,∴
,∴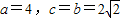 .
.
∴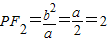 ,圆心Q(0,1),半径为3,x2+(y-1)2=9.
,圆心Q(0,1),半径为3,x2+(y-1)2=9.
(3)椭圆方程是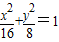 ,右准线方程为
,右准线方程为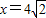 ,
,
∵直线AM,AN是圆Q的两条切线,∴切点M,N在以AQ为直径的圆上.设A点坐标为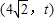 ,
,
∴该圆方程为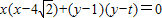 .∴直线MN是两圆的公共弦,两圆方程相减得:
.∴直线MN是两圆的公共弦,两圆方程相减得: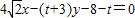 ,这就是直线MN的方程.
,这就是直线MN的方程.
该直线化为: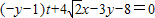 ,
,
∴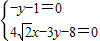 ,∴
,∴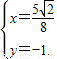
∴直线MN必过定点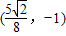 .
.
点评:本题考查直线 和圆锥曲线的位置关系的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.
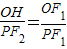 ,
,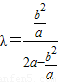 ,2a2λ-b2λ=b2,2a2λ=b2(1+λ),
,2a2λ-b2λ=b2,2a2λ=b2(1+λ),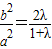 .
.(1)由
 ,知
,知 ,在
,在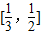 上单调递减.由此能求出椭圆的离心率e的取值范围.
上单调递减.由此能求出椭圆的离心率e的取值范围.(2)当
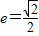 时,
时,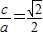 ,所以
,所以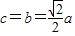 ,2b2=a2.由PF2⊥F1F2,知PF1是圆的直径,圆心是PF1的中点,由此能求出圆Q的方程.
,2b2=a2.由PF2⊥F1F2,知PF1是圆的直径,圆心是PF1的中点,由此能求出圆Q的方程.(3)椭圆方程是
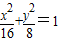 ,右准线方程为
,右准线方程为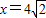 ,由直线AM,AN是圆Q的两条切线,知切点M,N在以AQ为直径的圆上.设A点坐标为
,由直线AM,AN是圆Q的两条切线,知切点M,N在以AQ为直径的圆上.设A点坐标为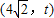 ,由此能够导出直线MN必过定点
,由此能够导出直线MN必过定点 .
.解答:解:由相似三角形知,
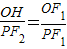 ,
,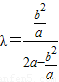 ,
,∴2a2λ-b2λ=b2,2a2λ=b2(1+λ),
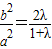 .
.(1)
 ,∴
,∴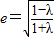 ,在
,在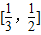 上单调递减.
上单调递减.∴
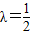 时,e2最小
时,e2最小 ,
,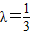 时,e2最大
时,e2最大 ,
,∴
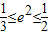 ,∴
,∴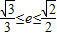 .
.(2)当
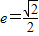 时,
时,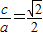 ,∴
,∴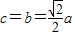 ,∴2b2=a2.
,∴2b2=a2.∵PF2⊥F1F2,∴PF1是圆的直径,圆心是PF1的中点,
∴在y轴上截得的弦长就是直径,∴PF1=6.
又
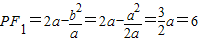 ,∴
,∴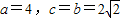 .
.∴
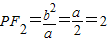 ,圆心Q(0,1),半径为3,x2+(y-1)2=9.
,圆心Q(0,1),半径为3,x2+(y-1)2=9.(3)椭圆方程是
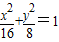 ,右准线方程为
,右准线方程为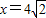 ,
,∵直线AM,AN是圆Q的两条切线,∴切点M,N在以AQ为直径的圆上.设A点坐标为
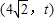 ,
,∴该圆方程为
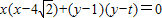 .∴直线MN是两圆的公共弦,两圆方程相减得:
.∴直线MN是两圆的公共弦,两圆方程相减得: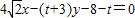 ,这就是直线MN的方程.
,这就是直线MN的方程.该直线化为:
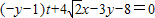 ,
,∴
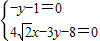 ,∴
,∴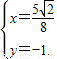
∴直线MN必过定点
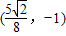 .
.点评:本题考查直线 和圆锥曲线的位置关系的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
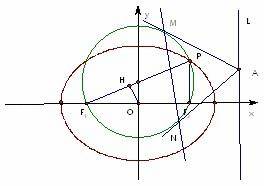
 左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,
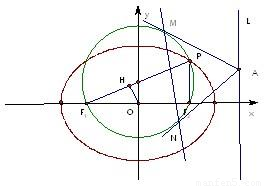
左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,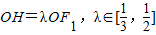 .
.
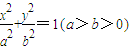 左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,
左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,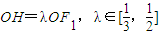 .
.
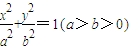 左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,
左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,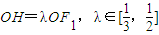 .
.