题目内容
定长为3的线段AB两端点A、B分别在x轴,y轴上滑动,M在线段AB上,且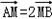 .
.
(1)求点M的轨迹C的方程;
(2)设过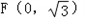 且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
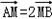 .
.(1)求点M的轨迹C的方程;
(2)设过
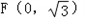 且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.解:(1)设A(x1,0),B(0,y1),M(x,y)
则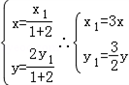 ,
,
|AB|=3= =1
=1
(2)存在满足条件的D点.
设满足条件的点D(0,m),则 ,
,
设l的方程为:y=kx+ ,(k≠0),
,(k≠0),
代入椭圆方程,得(k2+4)x2+2 kx﹣1=0,
kx﹣1=0,
设A(x1,y1),B(x2,y2),则x1+x2=﹣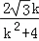 ,
,
∴y1+y2=k(x1+x2)+2 .
.
∵以DA、DB为邻边的平行四边形为菱形,
∴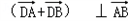 ,
,
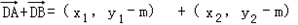 =
= ,
,
 的方向向量为(1,k),
的方向向量为(1,k),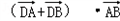 =0,
=0,
∴﹣ ﹣2mk=0即m=
﹣2mk=0即m=
∵k2>0,
∴m= ,
,
∴0<m< ,
,
∴存在满足条件的点D.
则
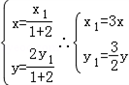 ,
,|AB|=3=
 =1
=1(2)存在满足条件的D点.
设满足条件的点D(0,m),则
 ,
,设l的方程为:y=kx+
 ,(k≠0),
,(k≠0),代入椭圆方程,得(k2+4)x2+2
 kx﹣1=0,
kx﹣1=0,设A(x1,y1),B(x2,y2),则x1+x2=﹣
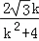 ,
,∴y1+y2=k(x1+x2)+2
 .
.∵以DA、DB为邻边的平行四边形为菱形,
∴
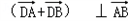 ,
,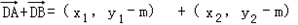 =
= ,
, 的方向向量为(1,k),
的方向向量为(1,k),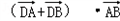 =0,
=0,∴﹣
 ﹣2mk=0即m=
﹣2mk=0即m=
∵k2>0,
∴m=
 ,
,∴0<m<
 ,
,∴存在满足条件的点D.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 轴,
轴, 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且
 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段 上
上 轴,
轴, 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且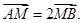
 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段 上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。
上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。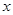 轴,
轴,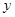 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且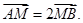
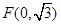 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线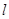 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段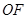 上
上