题目内容
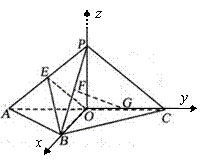
(09浙江理20)如图,平面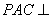 平面
平面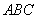 ,
,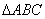 是以
是以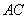 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 分别为
分别为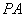 ,
, ,
,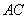 的中点,
的中点,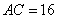 ,
,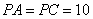 .
.
(I)设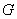 是
是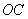 的中点,证明:
的中点,证明: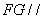 平面
平面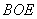 ;
;
(II)证明:在 内存在一点
内存在一点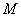 ,使
,使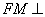 平面
平面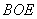 ,并求点
,并求点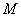 到
到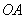 ,
,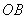 的距离.
的距离.

【答案】
证明:(I)如图,连结OP,以O为坐标原点,分别以OB、OC、OP所在直线为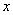 轴,
轴,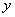 轴,
轴,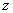 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O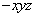 ,www.7caiedu.cn
,www.7caiedu.cn
则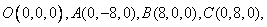
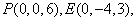
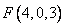 ,.c.o. 3分
,.c.o. 3分
由题意得,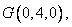 因
因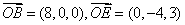 ,
,
因此平面BOE的法向量为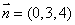 ,
,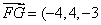
得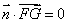 ,又直线
,又直线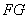 不在平面
不在平面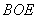 内,因此有
内,因此有
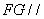 平面
平面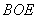 .c.o.m 6分
.c.o.m 6分
(II)设点M的坐标为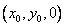 ,则
,则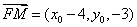 ,
,
因为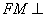 平面BOE,
平面BOE,
所以有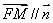 ,因此有
,因此有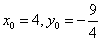 ,
,
即点M的坐标为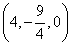 ,.c.o.m 8分
,.c.o.m 8分
在平面直角坐标系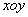 中,
中,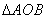 的内部区域满足不等式组
的内部区域满足不等式组 ,
,
经检验,点M的坐标满足上述不等式组,
所以在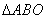 内存在一点
内存在一点 ,使
,使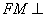 平面
平面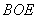 ,
,
由点M的坐标得点 到
到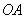 ,
,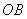 的距离为
的距离为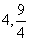 .www.7caiedu.cn
12分
.www.7caiedu.cn
12分

练习册系列答案
相关题目