题目内容
已知A、B、C是△ABC的三个内角,向量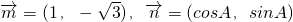 ,且
,且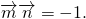
(1)求角A;
(2)若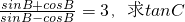 的值.
的值.
解:(1)因为 ,
,
所以 ,(2分)
,(2分)
所以 (4分)
(4分)
因为 (6分)
(6分)
(2)因为 ,
,
所以 (8分)
(8分)
所以tanB=2(9分)
所以tanC=tan(π-(A+B))=-tan(A+B)= ,(11分)
,(11分)
即 (12分)
(12分)
分析:(1)利用 ,直接得到A的关系式,利用两角差的余弦函数,求出A的值,注意A是三角形内角.
,直接得到A的关系式,利用两角差的余弦函数,求出A的值,注意A是三角形内角.
(2)根据 ,利用C=π-(A+B),利用诱导公式,通过两角和的正切,求出tanC的值.
,利用C=π-(A+B),利用诱导公式,通过两角和的正切,求出tanC的值.
点评:本题是基础题,考查三角恒等变换,利用向量数量积,注意三角形的内角的范围,求出角的大小,三角形中:A+B+C=π是常用结论.
 ,
,所以
 ,(2分)
,(2分)所以
 (4分)
(4分)因为
 (6分)
(6分)(2)因为
 ,
,所以
 (8分)
(8分)所以tanB=2(9分)
所以tanC=tan(π-(A+B))=-tan(A+B)=
 ,(11分)
,(11分)即
 (12分)
(12分)分析:(1)利用
 ,直接得到A的关系式,利用两角差的余弦函数,求出A的值,注意A是三角形内角.
,直接得到A的关系式,利用两角差的余弦函数,求出A的值,注意A是三角形内角.(2)根据
 ,利用C=π-(A+B),利用诱导公式,通过两角和的正切,求出tanC的值.
,利用C=π-(A+B),利用诱导公式,通过两角和的正切,求出tanC的值.点评:本题是基础题,考查三角恒等变换,利用向量数量积,注意三角形的内角的范围,求出角的大小,三角形中:A+B+C=π是常用结论.

练习册系列答案
相关题目
 β,则a∥b; ④若a与b异面,且a∥β,则b与β相交;
β,则a∥b; ④若a与b异面,且a∥β,则b与β相交;