题目内容
已知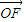 =(c,0)(c>0),
=(c,0)(c>0),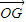 =(n,n)(n∈R),|
=(n,n)(n∈R),|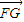 |的最小值为1,若动点P同时满足下列三个条件:
|的最小值为1,若动点P同时满足下列三个条件:①|
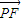 |=
|=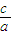 |
|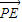 |(a>c>0);
|(a>c>0);②
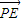 =λ
=λ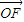 (其中
(其中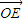 =(
=(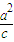 ,t),λ≠0,t∈R);
,t),λ≠0,t∈R);③动点P的轨迹C经过点B(0,-1).
(Ⅰ)求c的值;
(Ⅱ)求曲线C的方程;
(Ⅲ)是否存在方向向量为a=(1,k)(k≠0)的直线l,使l与曲线C交于两个不同的点M、N,且|
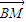 |=|
|=|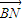 |?若存在,求出k的范围;若不存在,请说明理由.
|?若存在,求出k的范围;若不存在,请说明理由.
【答案】分析:(Ⅰ):由向量模的公式得出|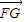 |=
|=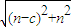 =
=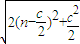 ,利用二次函数的性质得出其最小值,从而求得c值.
,利用二次函数的性质得出其最小值,从而求得c值.
(Ⅱ)先根据条件得到:|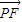 |=
|=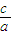 |
|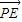 |(a>c>0).从而得出点P在以F为焦点,x=
|(a>c>0).从而得出点P在以F为焦点,x=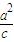 为准线的椭圆上,从而
为准线的椭圆上,从而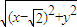 =
=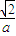 |
|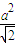 -x|,最后将点B(0-1)代入,解得a即可写出曲线C的方程;
-x|,最后将点B(0-1)代入,解得a即可写出曲线C的方程;
(Ⅲ)对于存在性问题,可先假设存在,即假设存在方向向量为a=(1,k)(k≠0)的直线l满足条件,则可设l:y=kx+m(k≠0),再利用△ABC为正三角形,求出CD的长,若出现矛盾,则说明假设不成立,即不存在;否则存在.
假设存在方向向量为a=(1,k)(k≠0)的直线l满足条件,则可设l:y=kx+m(k≠0),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系结合垂直关系即可求得k的范围,从而解决问题.
解答:解:(Ⅰ):|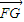 |=
|=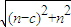 =
=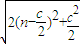 ,
,
当n=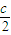 时,|
时,|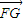 |min=
|min=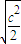 =1,所以c=
=1,所以c=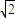 .(3分)
.(3分)
(Ⅱ)∵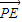 =λ
=λ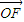 (λ≠0),∴PE⊥直线x=
(λ≠0),∴PE⊥直线x=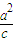 ,又|
,又|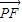 |=
|=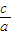 |
|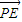 |(a>c>0).
|(a>c>0).
∴点P在以F为焦点,x=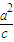 为准线的椭圆上.(5分)
为准线的椭圆上.(5分)
设P(x,y),则有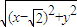 =
=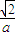 |
|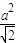 -x|,点B(0-1)代入,解得a=
-x|,点B(0-1)代入,解得a=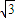 .
.
∴曲线C的方程为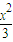 +y2=1 (7分)
+y2=1 (7分)
(Ⅲ)假设存在方向向量为a=(1,k)(k≠0)的直线l满足条件,则可设l:y=kx+m(k≠0),
与椭圆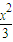 +y2=1联立,消去y得(1+3k2)x2+6kmx+3m2-3=0.(10分)
+y2=1联立,消去y得(1+3k2)x2+6kmx+3m2-3=0.(10分)
由判别式△>0,可得m2<3k2+1.①
设M(x1,y1),N(x2,y2),MN的中点P(x,y),由|BM|=|BN|,则有BP⊥MN.
由韦达定理代入kBP=-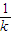 ,可得到m=
,可得到m=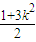 ②
②
联立①②,可得到 k2-1<0,(12分)
∵k≠0,∴-1<k<0或0<k1.
即存在k∈(-1,0)∪(0,1),使l与曲线C交于两个不同的点M、N,且|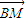 |=|
|=|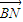 |.(14分)z
|.(14分)z
点评:本小题主要考查向量在几何中的应用、直线与圆锥曲线的综合问题,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
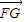 |=
|=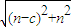 =
=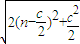 ,利用二次函数的性质得出其最小值,从而求得c值.
,利用二次函数的性质得出其最小值,从而求得c值.(Ⅱ)先根据条件得到:|
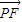 |=
|=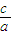 |
|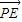 |(a>c>0).从而得出点P在以F为焦点,x=
|(a>c>0).从而得出点P在以F为焦点,x=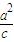 为准线的椭圆上,从而
为准线的椭圆上,从而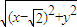 =
=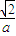 |
|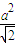 -x|,最后将点B(0-1)代入,解得a即可写出曲线C的方程;
-x|,最后将点B(0-1)代入,解得a即可写出曲线C的方程;(Ⅲ)对于存在性问题,可先假设存在,即假设存在方向向量为a=(1,k)(k≠0)的直线l满足条件,则可设l:y=kx+m(k≠0),再利用△ABC为正三角形,求出CD的长,若出现矛盾,则说明假设不成立,即不存在;否则存在.
假设存在方向向量为a=(1,k)(k≠0)的直线l满足条件,则可设l:y=kx+m(k≠0),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系结合垂直关系即可求得k的范围,从而解决问题.
解答:解:(Ⅰ):|
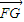 |=
|=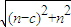 =
=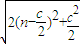 ,
,当n=
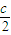 时,|
时,|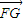 |min=
|min=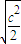 =1,所以c=
=1,所以c=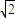 .(3分)
.(3分)(Ⅱ)∵
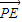 =λ
=λ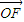 (λ≠0),∴PE⊥直线x=
(λ≠0),∴PE⊥直线x=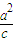 ,又|
,又|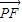 |=
|=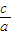 |
|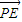 |(a>c>0).
|(a>c>0).∴点P在以F为焦点,x=
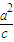 为准线的椭圆上.(5分)
为准线的椭圆上.(5分)设P(x,y),则有
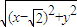 =
=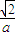 |
|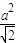 -x|,点B(0-1)代入,解得a=
-x|,点B(0-1)代入,解得a=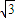 .
.∴曲线C的方程为
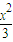 +y2=1 (7分)
+y2=1 (7分)(Ⅲ)假设存在方向向量为a=(1,k)(k≠0)的直线l满足条件,则可设l:y=kx+m(k≠0),
与椭圆
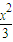 +y2=1联立,消去y得(1+3k2)x2+6kmx+3m2-3=0.(10分)
+y2=1联立,消去y得(1+3k2)x2+6kmx+3m2-3=0.(10分)由判别式△>0,可得m2<3k2+1.①
设M(x1,y1),N(x2,y2),MN的中点P(x,y),由|BM|=|BN|,则有BP⊥MN.
由韦达定理代入kBP=-
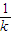 ,可得到m=
,可得到m=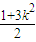 ②
②联立①②,可得到 k2-1<0,(12分)
∵k≠0,∴-1<k<0或0<k1.
即存在k∈(-1,0)∪(0,1),使l与曲线C交于两个不同的点M、N,且|
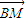 |=|
|=|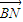 |.(14分)z
|.(14分)z点评:本小题主要考查向量在几何中的应用、直线与圆锥曲线的综合问题,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知直线x-2y+2=0经过椭圆
已知直线x-2y+2=0经过椭圆 +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径
与以原点为圆心,以椭圆C的短半轴长为半径 ,0)求实数k的取值范围。
,0)求实数k的取值范围。