题目内容
已知f(x)=2cos
(
sin
+cos
)-1,x∈R.
(1)求f(x)的最小正周期;
(2)设α、β∈(0,
),f(α)=2,f(β)=
,求f(α+β)的值.
| x |
| 2 |
| 3 |
| x |
| 2 |
| x |
| 2 |
(1)求f(x)的最小正周期;
(2)设α、β∈(0,
| π |
| 2 |
| 8 |
| 5 |
(1)f(x)=2
sin
cos
+2cos2
-1=
sinx+cosx=2sin(x+
),
∵ω=1,
∴f(x)的最小正周期T=2π;
(2)∵f(α)=2sin(α+
)=2,
即sin(α+
)=1,
∵
<α+
<
,
∴α+
=
,
即α=
,
∵f(β)=2sin(β+
)=
,
即sin(β+
)=
<
,
∴
<β+
<
,cos(β+
)=
,
则f(α+β)=2sin(α+β+
)=2sin(
+β)=2cosβ=2cos[(β+
)-
]=2cos(β+
)cos
+2sin(β+
)sin
=
.
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 3 |
| π |
| 6 |
∵ω=1,
∴f(x)的最小正周期T=2π;
(2)∵f(α)=2sin(α+
| π |
| 6 |
即sin(α+
| π |
| 6 |
∵
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
∴α+
| π |
| 6 |
| π |
| 2 |
即α=
| π |
| 3 |
∵f(β)=2sin(β+
| π |
| 6 |
| 8 |
| 5 |
即sin(β+
| π |
| 6 |
| 4 |
| 5 |
| ||
| 2 |
∴
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| 3 |
| 5 |
则f(α+β)=2sin(α+β+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
3
| ||
| 5 |

练习册系列答案
相关题目
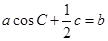 .
.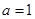 ,求△ABC的周长L的取值范围.
,求△ABC的周长L的取值范围.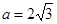 ,
,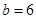 ,
,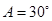 ,求B及S
,求B及S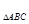 .
.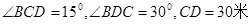 ,并在点C测得塔顶A的仰角为
,并在点C测得塔顶A的仰角为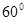 ,求塔高AB.
,求塔高AB.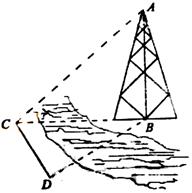
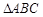 中,
中,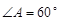 ,
,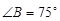 ,
,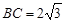 ,则
,则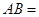 .
.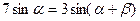 ,求证:
,求证: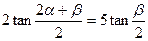 .
.