题目内容
![]()
![]()
![]()
已知曲线![]() ,点
,点![]() 是曲线
是曲线![]() 上的点(n=1,2,…).
上的点(n=1,2,…).
(1)试写出曲线![]() 在点
在点![]() 处的切线
处的切线![]() 的方程,并求出
的方程,并求出![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标;
的坐标;
(2)若原点![]() 到
到![]() 的距离与线段
的距离与线段![]() 的长度之比取得最大值,试求点
的长度之比取得最大值,试求点![]() 的坐标
的坐标![]() ;
;
(3)设![]() 与
与![]() 为两个给定的不同的正整数,
为两个给定的不同的正整数,![]() 与
与![]() 是满足(2)中条件的点
是满足(2)中条件的点![]() 的坐标,
的坐标,
证明:
![]()
.解:(1)![]() ,设切线
,设切线![]() 的斜率为
的斜率为![]() ,则
,则
![]()
∴曲线![]() 在点
在点![]() 处的切线
处的切线![]() 的方程为:
的方程为:![]()
又∵点![]() 在曲线
在曲线![]() 上, ∴
上, ∴![]()
∴曲线![]() 在点
在点![]() 处的切线
处的切线![]() 的方程为:
的方程为:![]() 即
即![]()
令![]() 得
得![]() ,∴曲线
,∴曲线![]() 在
在![]() 轴上的交点
轴上的交点![]() 的坐标为
的坐标为![]()
(2)原点![]() 到直线
到直线![]() 的距离与线段
的距离与线段![]()
![]() 的长度之比为:
的长度之比为:

当且仅当![]() 即
即![]() 时,取等号。此时,
时,取等号。此时,![]()
故点![]() 的坐标为
的坐标为![]()
(3)证法一:要证![]()
只要证![]()
只要证![]()
![]() ,又
,又![]()
![]()
所以:![]()
![]()
证法二:由上知,只需证![]() ,
,
又![]()
![]() ,故只需证
,故只需证![]() ,可用数学归纳法证明之
,可用数学归纳法证明之

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
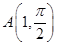 ,点
,点 是曲线
是曲线 上任意一点,设点
上任意一点,设点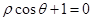 的距离为
的距离为 ,则
,则 的最小值为 .
的最小值为 . ,点
,点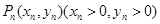 是曲线
是曲线 上的点
上的点 .
. 处的切线
处的切线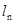 的方程,并求出
的方程,并求出 轴的交点
轴的交点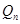 的坐标;
的坐标; 到
到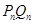 的长度之比取得最大值,试求试点
的长度之比取得最大值,试求试点 ;
; 与
与 为两个给定的不同的正整数,
为两个给定的不同的正整数,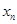 与
与 是满足(2)中条件的点
是满足(2)中条件的点
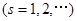
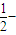 伴随切线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.
伴随切线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.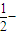 伴随切线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.
伴随切线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.