题目内容
定义一种新运算:
?
=|
||
|sinθ,其中θ为
与
的夹角.已知
=(-
,1),
=(
,0),则
?
=
.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| 3 |
| b |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
分析:根据新定义,需求出|
|,|
|,及sinθ,前两者以求,为求sinθ,可利用向量夹角公式求得cosθ,再利用同角三角函数基本关系式求出sinθ.
| a |
| b |
解答:解:|
|=
=2,|
|=
=
,
•
=-
由向量夹角公式得cosθ=
=-
,θ=150°∴sinθ=
,
∴
?
=|
||
|sinθ=2×
×
=
,
故答案为:
| a |
(-
|
| b |
(
|
| 1 |
| 2 |
| a |
| b |
| ||
| 2 |
由向量夹角公式得cosθ=
| ||||
|
|
| ||
| 2 |
| 1 |
| 2 |
∴
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题是新定义型题目.考查向量模、夹角的计算.对于新定义题型,题目中会出现一些符号或运算法则是教材中不曾介绍过的内容,但我们只要根据题中所给的条件,理解题目给出的信息是什么,结合已学过的知识,一般都能解决.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
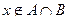 },又已知A={0,1,2,},B={1,2,3
},又已知A={0,1,2,},B={1,2,3 },用列举法写出A*B=
},用列举法写出A*B= 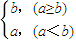 已知函数f(x)=(1+
已知函数f(x)=(1+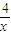 )•log2x,若函数g(x)=f(x)-k恰有两个零点,则k的取值范围为( )
)•log2x,若函数g(x)=f(x)-k恰有两个零点,则k的取值范围为( )