题目内容
设P为抛物线y2=2px(p>0)上任意一点,F为抛物线焦点,定点A(1,3),且|PA|+|PF|的最小值为 ,则抛物线方程为( )
,则抛物线方程为( )A.y2=2(
 )
)B.y2=4
C.y2=8
D.y2=4(
 )
)
【答案】分析:分类讨论,A(1,3)在抛物线内,则|PA|+|PF|的最小值为1+ =
=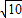 ;A(1,3)在抛物线外,则|PA|+|PF|的最小值为|AF|,由此可得结论.
;A(1,3)在抛物线外,则|PA|+|PF|的最小值为|AF|,由此可得结论.
解答:解:若A(1,3)在抛物线内,则|PA|+|PF|的最小值为1+ =
= ,∴2p=4(
,∴2p=4( ),∴方程为y2=4(
),∴方程为y2=4( )x,此时(1,3)在抛物线外,不合题意;
)x,此时(1,3)在抛物线外,不合题意;
若A(1,3)在抛物线外,则|PA|+|PF|的最小值为|AF|=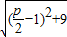 =
= ,∴p=4,∴方程为y2=8x,此时(1,3)在抛物线外,符合题意;
,∴p=4,∴方程为y2=8x,此时(1,3)在抛物线外,符合题意;
故选C.
点评:本题考查抛物线的定义,考查学生的计算能力、分类讨论的思想,属于中档题.
 =
=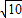 ;A(1,3)在抛物线外,则|PA|+|PF|的最小值为|AF|,由此可得结论.
;A(1,3)在抛物线外,则|PA|+|PF|的最小值为|AF|,由此可得结论.解答:解:若A(1,3)在抛物线内,则|PA|+|PF|的最小值为1+
 =
= ,∴2p=4(
,∴2p=4( ),∴方程为y2=4(
),∴方程为y2=4( )x,此时(1,3)在抛物线外,不合题意;
)x,此时(1,3)在抛物线外,不合题意;若A(1,3)在抛物线外,则|PA|+|PF|的最小值为|AF|=
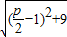 =
= ,∴p=4,∴方程为y2=8x,此时(1,3)在抛物线外,符合题意;
,∴p=4,∴方程为y2=8x,此时(1,3)在抛物线外,符合题意;故选C.
点评:本题考查抛物线的定义,考查学生的计算能力、分类讨论的思想,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目