题目内容
平面内动点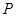 到点
到点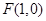 的距离等于它到直线
的距离等于它到直线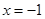 的距离,记点
的距离,记点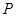 的轨迹为曲
的轨迹为曲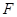 .
.
(Ⅰ)求曲线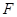 的方程;
的方程;
(Ⅱ)若点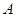 ,
,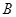 ,
,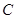 是
是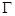 上的不同三点,且满足
上的不同三点,且满足 .证明:
.证明: 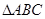 不可能为直角三角形.
不可能为直角三角形.
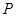 到点
到点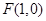 的距离等于它到直线
的距离等于它到直线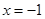 的距离,记点
的距离,记点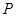 的轨迹为曲
的轨迹为曲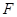 .
.(Ⅰ)求曲线
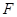 的方程;
的方程;(Ⅱ)若点
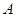 ,
,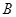 ,
,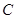 是
是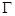 上的不同三点,且满足
上的不同三点,且满足 .证明:
.证明: 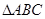 不可能为直角三角形.
不可能为直角三角形.(1)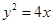
(2)利用向量的关系式来得到坐标关系式,然后借助于反证法来说明不成立。
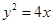
(2)利用向量的关系式来得到坐标关系式,然后借助于反证法来说明不成立。
试题分析:解法一:(Ⅰ)由条件可知,点
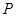 到点
到点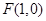 的距离与到直线
的距离与到直线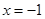 的距离相等, 所以点
的距离相等, 所以点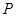 的轨迹是以
的轨迹是以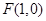 为焦点,
为焦点,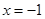 为准线的抛物线,其方程为
为准线的抛物线,其方程为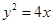 . 4分
. 4分(Ⅱ)假设
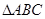 是直角三角形,不失一般性,设
是直角三角形,不失一般性,设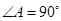 ,
,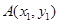 ,
,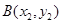 ,
,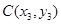 ,则由
,则由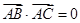 ,
,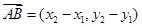 ,
,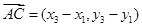 ,
,所以
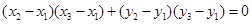 . 6分
. 6分因为
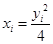
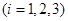 ,
,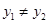 ,
,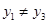 ,
,所以
 . 8分
. 8分又因为
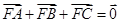 ,所以
,所以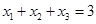 ,
,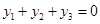 ,
,所以
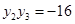 . ①
. ①又
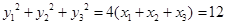 ,
,所以
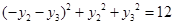 ,即
,即 . ② 10分
. ② 10分由①,②得
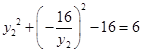 ,所以
,所以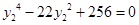 . ③
. ③因为
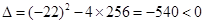 .
.所以方程③无解,从而
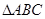 不可能是直角三角形. 12分
不可能是直角三角形. 12分解法二:(Ⅰ)同解法一
(Ⅱ)设
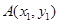 ,
,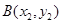 ,
,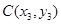 ,由
,由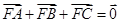 ,
,得
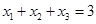 ,
,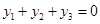 . 6分
. 6分由条件的对称性,欲证
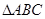 不是直角三角形,只需证明
不是直角三角形,只需证明 .
.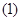 当
当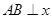 轴时,
轴时,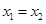 ,
,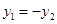 ,从而
,从而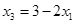 ,
,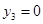 ,
,即点
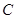 的坐标为
的坐标为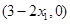 .
.由于点
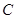 在
在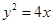 上,所以
上,所以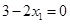 ,即
,即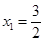 ,
,此时
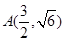 ,
,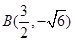 ,
, ,则
,则 . 8分
. 8分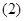 当
当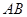 与
与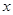 轴不垂直时,
轴不垂直时,设直线
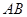 的方程为:
的方程为: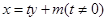 ,代入
,代入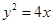 ,
,整理得:
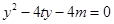 ,则
,则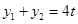 .
.若
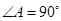 ,则直线
,则直线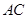 的斜率为
的斜率为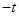 ,同理可得:
,同理可得: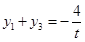 .
.由
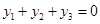 ,得
,得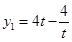 ,
,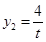 ,
,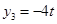 .
.由
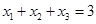 ,可得
,可得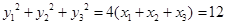 .
.从而
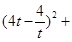
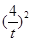
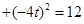 ,
,整理得:
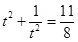 ,即
,即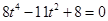 ,①
,① .
.所以方程①无解,从而
 . 11分
. 11分综合
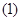 ,
,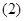 ,
, 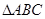 不可能是直角三角形. 12分
不可能是直角三角形. 12分点评:本小题考查抛物线的标准方程、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想、数形结合思想等

练习册系列答案
相关题目
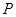 到两点
到两点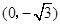 ,
,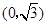 的距离之和等于4,设点
的距离之和等于4,设点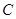 ,直线
,直线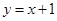 与轨迹
与轨迹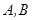 两点.
两点.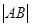 的值.
的值.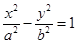
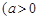 ,
,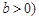 的左焦点
的左焦点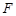 作圆
作圆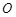 :
: 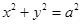 的两条切线,切点为
的两条切线,切点为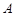 ,
,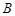 ,双曲线左顶点为
,双曲线左顶点为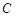 ,若
,若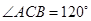 ,则双曲线的渐近线方程为 ( )
,则双曲线的渐近线方程为 ( )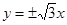
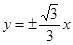
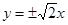
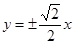
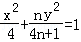 围成的区域(含边界)为Ωn(n=1,2,…),当点(x,y)分别在Ω1,Ω2,…上时,x+y的最大值分别是M1,M2,…,则
围成的区域(含边界)为Ωn(n=1,2,…),当点(x,y)分别在Ω1,Ω2,…上时,x+y的最大值分别是M1,M2,…,则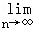 Mn=( )
Mn=( )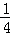
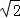
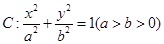 的焦距为4,且过点
的焦距为4,且过点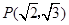 .
.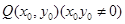 为椭圆
为椭圆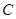 上一点,过点
上一点,过点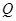 作
作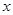 轴的垂线,垂足为
轴的垂线,垂足为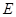 。取点
。取点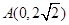 ,连接
,连接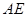 ,过点
,过点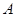 作
作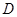 。点
。点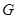 是点
是点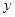 轴的对称点,作直线
轴的对称点,作直线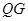 ,问这样作出的直线
,问这样作出的直线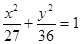 有相同焦点,且经过点
有相同焦点,且经过点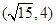 ,求其方程。
,求其方程。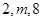 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线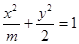 的离心率为( )
的离心率为( )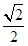
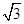

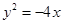 的准线方程是 .
的准线方程是 .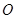 为几点,
为几点, 轴的正半轴为极轴建立极坐标系.已知直线
轴的正半轴为极轴建立极坐标系.已知直线 上两点
上两点 的极坐标分别为
的极坐标分别为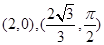 ,圆
,圆 的参数方程
的参数方程 (
( 为参数).
为参数).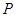 为线段
为线段 的中点,求直线
的中点,求直线 的平面直角坐标方程;
的平面直角坐标方程;