题目内容
空间9个点分布在异面直线l1、l2上,l1有4个点,l2上5个点,则由它们可确定异面直线 ( )
 180对 B.21对 C.121对 D.60对
180对 B.21对 C.121对 D.60对
 180对 B.21对 C.121对 D.60对
180对 B.21对 C.121对 D.60对C
设L1上的4点为A、B、C、D,L2上的5点为E、F、G、H、M,在L1上的4点中任取2点有6种选择,假设选择A、B,在L2上的5点中任取2点有10种选择,假设选择E、F,则AE、BF为一对异面直线,AF、BE为一对异面直线(AB、EF即为直线L1、L2单独考虑),所以不考虑L1、L2一共有6×10×2=120对,加上L1、L2也是一对,一共121对异面直线。所以选C。

练习册系列答案
相关题目
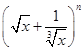 的展开式中的各项系数之和大于
的展开式中的各项系数之和大于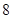 ,小于
,小于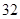 ,则展开式中系数最大的项是( )
,则展开式中系数最大的项是( )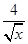
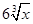
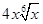
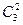 ·
·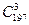 +
+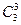 ·
·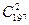
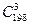
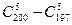
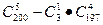
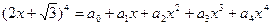 ,则
,则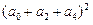
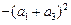 的值为 。
的值为 。 的二项展开式中第4项是 .
的二项展开式中第4项是 .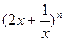 的展开式中第m项的系数为
的展开式中第m项的系数为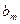 ,若
,若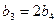 ,则
,则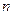 =__________.
=__________.