题目内容
已知点(1,3)、(an,an+1)(n∈N*)都在函数f(x)=px+2(p为常数)的图象上,a1=1,数列{bn}满足:bn=an+
(n∈N*).
(I)求数列{an}的通项公式;
(II)求数列{bn}的前n项和Sn.
| 1 | n(n+1) |
(I)求数列{an}的通项公式;
(II)求数列{bn}的前n项和Sn.
分析:(I)将点(1,3)、(an,an+1)代入f(x)=px+2,可得数列{an}是以2为公差的等差数列,从而可得结论;
(II)利用分组求和,可得结论.
(II)利用分组求和,可得结论.
解答:解:(I)∵点(1,3)、(an,an+1)在f(x)=px+2的图象上
∴3=p+2,an+1=pan+2
∴p=1,an+1-an=2
∴数列{an}是以2为公差的等差数列,
∵a1=1,d=2,∴an=a1+(n-1)d=2n-1;
(II)∵bn=an+
=2n-1+(
-
)
∴Sn=[1+3+…+(2n-1)]+[(1-
)+(
-
)+…+(
-
)]=n2+
.
∴3=p+2,an+1=pan+2
∴p=1,an+1-an=2
∴数列{an}是以2为公差的等差数列,
∵a1=1,d=2,∴an=a1+(n-1)d=2n-1;
(II)∵bn=an+
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=[1+3+…+(2n-1)]+[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查等差数列的判断,考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
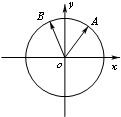 如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点. 如图:在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A、B两点.
如图:在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A、B两点. 如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点.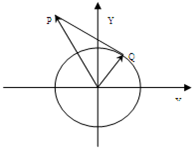 已知点
已知点