题目内容
已知{bn}是公比大于1的等比数列，它的前n项和为Sn，若S3=14，b1+8，3b2，b3+6成等差数列，且a1=1，
（n≥2）．
（1）求bn；
（2）求数列{nan}的前n项和Sn．
解：（1）依S3=14，b1+8，3b2，b3+6成等差数列，
得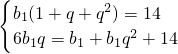
（2分）
从而2q2-5q+2=0得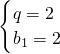
故bn=2n．（4分）
（2）当n≥2时，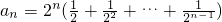
=2n-2
则Sn=a1+2a2+3a3+…+nan=1+2（22-2）+3（23-2）+…+n（2n-2）
=1+（2×22+3×23+…+n×2n）-2（2+3+…+n）（1分）
令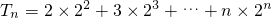
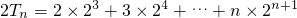
得
=（1-n）•2n+1
故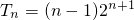
．（3分）
于是Sn=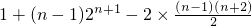
=（n-1）•2n+1-n2-n+3．（2分）
分析：（1）利用S3=14，b1+8，3b2，b3+6成等差数列，求出公比与首项，推出通项公式．
（2）利用（1）推出的表达式，通过错位相减法求数列{nan}的前n项和Sn．
点评：本题考查等差数列与等比数列的综合应用，数列通项公式的求法，前n项和的求法，考查分析问题解决问题的能力．
得
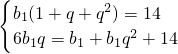（2分）从而2q2-5q+2=0得
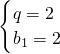
故bn=2n．（4分）
（2）当n≥2时，
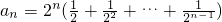=2n-2则Sn=a1+2a2+3a3+…+nan=1+2（22-2）+3（23-2）+…+n（2n-2）
=1+（2×22+3×23+…+n×2n）-2（2+3+…+n）（1分）
令
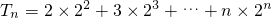
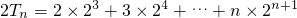
得
=（1-n）•2n+1故
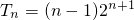．（3分）于是Sn=
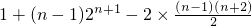=（n-1）•2n+1-n2-n+3．（2分）分析：（1）利用S3=14，b1+8，3b2，b3+6成等差数列，求出公比与首项，推出通项公式．
（2）利用（1）推出
的表达式，通过错位相减法求数列{nan}的前n项和Sn．点评：本题考查等差数列与等比数列的综合应用，数列通项公式的求法，前n项和的求法，考查分析问题解决问题的能力．
练习册系列答案
相关题目