题目内容
若双曲线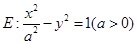 的离心率等于
的离心率等于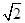 ,直线
,直线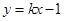 与双曲线
与双曲线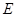 的右支交于
的右支交于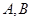 两点.
两点.
(1)求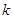 的取值范围;
的取值范围;
(2)若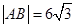 ,点
,点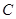 是双曲线
是双曲线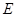 上一点,且
上一点,且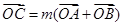 ,求
,求
【答案】
(1)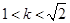 (2)
(2)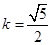 ,
,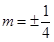
【解析】
试题分析:(1)由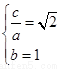 得
得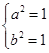
故双曲线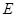 的方程为
的方程为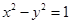 2分
2分
设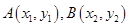 ,
,
由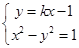 得
得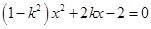 4分
4分
又直线与双曲线右支交于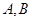 两点,所以
两点,所以
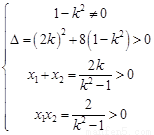 解得
解得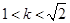 -----6分
-----6分
(2)
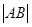
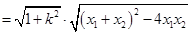
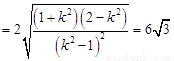
得 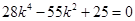
∴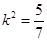 或
或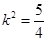 又
又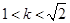 ∴
∴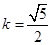 9分
9分
那么 ,
,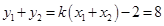
设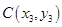 ,由已知
,由已知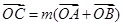 ,得
,得
∴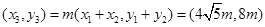
∴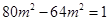 ,得
,得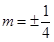
故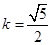 ,
,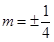 .----------14分
.----------14分
考点:双曲线方程及性质,直线与双曲线的位置关系
点评:直线与双曲线相交时常联立方程组,转化为关于x或y的二次方程,利用韦达定理设而不求的方法
再将所求问题用根与系数的关系的表示

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若双曲线mx2-y2=1过抛物线y2=2x的焦点,则双曲线的离心率等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|