题目内容
已知点P在双曲线x2-y2=a2(a>0)的右支上,A1,A2分别是双曲线的左、右顶点,且∠A2PA1=2∠PA1A2,则∠PA1A2= .
【答案】分析:由题意设∠PA1A2=α,则∠PA2X=3α.利用坐标表示出PA1的斜率,PA2的斜率,借助于双曲线的方程得出斜率之积为1,从而可求.
解答:解:设∠PA1A2=α,则∠PA2X=3α.设P(x,y),A1(-a,0),A2(a,0).
PA1的斜率 k1=tanα=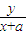 ,PA2的斜率 k2=tan3α=
,PA2的斜率 k2=tan3α=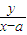
∵k1k2=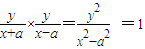 ,∴tanαtan3α=1,∴tan3α=cotα=tan(
,∴tanαtan3α=1,∴tan3α=cotα=tan(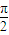 -α).
-α).
∵?3α是锐角,必有 3α=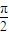 -α,∴?α=
-α,∴?α=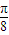 .
.
故答案为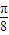 .
.
点评:本题主要考查直线的斜率与倾斜角的关系,解题时利用双曲线的方程得出斜率之积为1是关键.
解答:解:设∠PA1A2=α,则∠PA2X=3α.设P(x,y),A1(-a,0),A2(a,0).
PA1的斜率 k1=tanα=
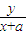 ,PA2的斜率 k2=tan3α=
,PA2的斜率 k2=tan3α=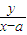
∵k1k2=
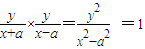 ,∴tanαtan3α=1,∴tan3α=cotα=tan(
,∴tanαtan3α=1,∴tan3α=cotα=tan(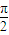 -α).
-α).∵?3α是锐角,必有 3α=
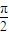 -α,∴?α=
-α,∴?α=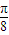 .
.故答案为
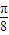 .
.点评:本题主要考查直线的斜率与倾斜角的关系,解题时利用双曲线的方程得出斜率之积为1是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目