题目内容
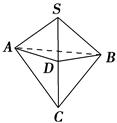
已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为________.
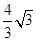
如图所示,由题意知,在棱锥S-ABC中,△SAC,△SBC都是等腰直角三角形,其中AB=2,SC=4,SA=AC=SB=BC=2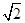 .取SC的中点D,易证SC垂直于面ABD,因此棱锥SABC的体积为两个棱锥S-ABD和C-ABD的体积和,所以棱锥S-ABC的体积V=
.取SC的中点D,易证SC垂直于面ABD,因此棱锥SABC的体积为两个棱锥S-ABD和C-ABD的体积和,所以棱锥S-ABC的体积V=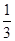 SC·S△ADB=
SC·S△ADB=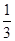 ×4×
×4×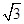 =
=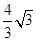
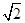 .取SC的中点D,易证SC垂直于面ABD,因此棱锥SABC的体积为两个棱锥S-ABD和C-ABD的体积和,所以棱锥S-ABC的体积V=
.取SC的中点D,易证SC垂直于面ABD,因此棱锥SABC的体积为两个棱锥S-ABD和C-ABD的体积和,所以棱锥S-ABC的体积V=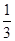 SC·S△ADB=
SC·S△ADB=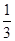 ×4×
×4×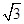 =
=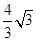


练习册系列答案
相关题目
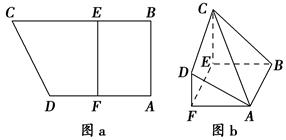
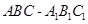 中,
中, ,
,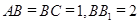 ,求:
,求: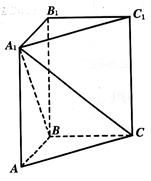
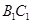 与
与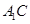 所成角的大小;
所成角的大小; 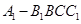 的体积.
的体积. =2,点G为AC的中点.
=2,点G为AC的中点.
 中,侧面
中,侧面 为矩形,
为矩形, ,
, ,
, 为
为 的中点,
的中点, 与
与 交于点
交于点 ,
, 侧面
侧面
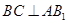 ;
; ,求三棱锥
,求三棱锥 的体积.
的体积.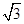 的正三角形,侧棱垂直于底面,且该三棱柱的外接球的体积为
的正三角形,侧棱垂直于底面,且该三棱柱的外接球的体积为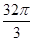 ,则该三棱柱的体积为________.
,则该三棱柱的体积为________.

