题目内容
设圆![]() 过点P(0,2), 且在
过点P(0,2), 且在![]() 轴上截得的弦RG的长为4.
轴上截得的弦RG的长为4.
(1)求圆心![]() 的轨迹E的方程;
的轨迹E的方程;
(2)过![]() 点
点![]() (0,1),作轨迹
(0,1),作轨迹![]() 的两条互相垂直的弦、
的两条互相垂直的弦、![]() ,设
,设![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() ,试判断直线
,试判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
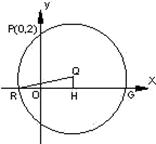
解:(1)设圆心![]() 的坐标为
的坐标为![]() ,如图过圆心
,如图过圆心![]() 作
作![]() 轴于H,
轴于H,
则H为RG的中点,在![]() 中,
中,![]() …3分
…3分
∵![]() ∴
∴![]()
即![]() …………………6分
…………………6分
(2) 设![]() ,
,![]()
直线AB的方程为![]() (
(![]() )则
)则![]() -----①
-----①![]() ---②
---②
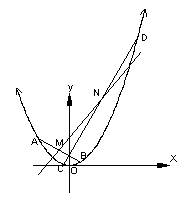 由①-②得
由①-②得![]() ,∴
,∴![]() ,………………9分
,………………9分
∵点![]() 在直线
在直线![]() 上, ∴
上, ∴![]() .
.
∴点M的坐标为![]() . ………………10分
. ………………10分
同理可得:![]() ,
, ![]() ,
,![]()
∴点![]() 的坐标为
的坐标为![]() . ………………11分
. ………………11分
直线![]() 的斜率为
的斜率为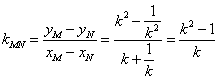 ,其方程为
,其方程为
![]() ,整理得
,整理得![]() ,………………13分
,………………13分
显然,不论![]() 为何值,点
为何值,点![]() 均满足方程,
均满足方程,
∴直线![]() 恒过定点
恒过定点![]() .……………………14分
.……………………14分

练习册系列答案
相关题目
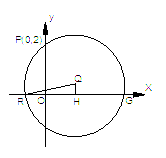 (本小题满分12分)设圆
(本小题满分12分)设圆
 题满分14分)
题满分14分) 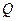 过点P(0,2), 且在
过点P(0,2), 且在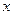 轴上截得的弦RG的长为4.
轴上截得的弦RG的长为4.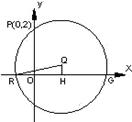
 点
点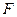 (0,1),作轨迹
(0,1),作轨迹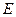 的两条互相垂直的弦
的两条互相垂直的弦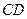 ,设
,设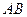 、
、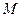 、
、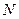 ,试判断直线
,试判断直线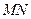 是否过定点?并说明理由.
是否过定点?并说明理由.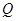 过点P(0,2), 且在
过点P(0,2), 且在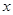 轴上截得的弦RG的长为4.
轴上截得的弦RG的长为4.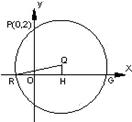
 (0,1),作轨迹
(0,1),作轨迹 的两条互相垂直的弦
的两条互相垂直的弦 ,设
,设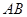 、
、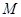 、
、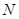 ,试判断直线
,试判断直线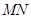 是否过定点?并说明理由.
是否过定点?并说明理由.