题目内容
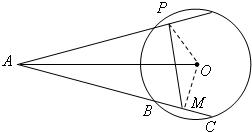
22、如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.
(Ⅰ)证明A,P,O,M四点共圆;
(Ⅱ)求∠OAM+∠APM的大小.

(Ⅰ)证明A,P,O,M四点共圆;
(Ⅱ)求∠OAM+∠APM的大小.

分析:(I)连接OP,OM,利用AP与⊙O相切于点P和M是⊙O的弦BC的中点得到垂直关系,从而证得四边形的对角互补,最后得到A,P,O,M四点共圆;
(II)由(Ⅰ)得A,P,O,M四点共圆得到∠OAM=∠OPM,及OP⊥AP,从而∠OPM+∠APM=90°,从而问题解决.
(II)由(Ⅰ)得A,P,O,M四点共圆得到∠OAM=∠OPM,及OP⊥AP,从而∠OPM+∠APM=90°,从而问题解决.
解答:解:(Ⅰ)证明:连接OP,OM.
因为AP与⊙O相切于点P,所以OP⊥AP.
因为M是⊙O的弦BC的中点,所以OM⊥BC.
于是∠OPA+∠OMA=180°.
由圆心O在∠PAC的内部,可知四边形的对角互补,
所以A,P,O,M四点共圆.
(Ⅱ)解:由(Ⅰ)得A,P,O,M四点共圆,所以∠OAM=∠OPM.
由(Ⅰ)得OP⊥AP.
由圆心O在∠PAC的内部,可知∠OPM+∠APM=90°.
所以∠OAM+∠APM=90°.
因为AP与⊙O相切于点P,所以OP⊥AP.
因为M是⊙O的弦BC的中点,所以OM⊥BC.
于是∠OPA+∠OMA=180°.
由圆心O在∠PAC的内部,可知四边形的对角互补,
所以A,P,O,M四点共圆.
(Ⅱ)解:由(Ⅰ)得A,P,O,M四点共圆,所以∠OAM=∠OPM.
由(Ⅰ)得OP⊥AP.
由圆心O在∠PAC的内部,可知∠OPM+∠APM=90°.
所以∠OAM+∠APM=90°.

点评:本小题主要考查与圆有关的比例线段、与圆有关的比例线段的应用、四点共圆的解法等基础知识,考查运算求解能力、化归与转化思想.属于基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 22、如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.
22、如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点. O的切线,P为切点,AC是
O的切线,P为切点,AC是 PAC的内部,点M是BC的中点。
PAC的内部,点M是BC的中点。
 如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在 的内部,点M是BC的中点.
的内部,点M是BC的中点. 如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.