题目内容
(本题满分14分)
在数列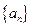 中,已知
中,已知
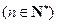 .
.
(1)求数列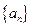 的通项公式;
的通项公式;
(2)求数列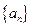 的前
的前 项和
项和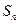 .
.
解:(1)解法1:由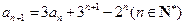
可得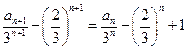 ,------------------------------3分
,------------------------------3分
∴数列 是首项为
是首项为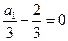 ,公差为1等差数列,
,公差为1等差数列,
∴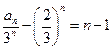 , -------------------------------------------------------------------------------6分
, -------------------------------------------------------------------------------6分
∴数列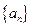 的通项公式为
的通项公式为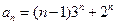 .-------------------------------------------------7分
.-------------------------------------------------7分
解法2:由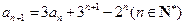
可得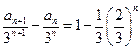 -------------------------------------------------------------------------2分
-------------------------------------------------------------------------2分
令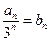 ,则
,则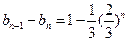 --------------------------------------------------------------3分
--------------------------------------------------------------3分
∴当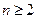 时
时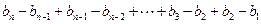
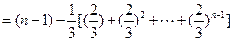 ----5分
----5分
∴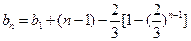
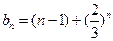 -------------------------------------------------------------------------------------6分
-------------------------------------------------------------------------------------6分
∴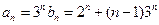 ------------------------------------------------7分
------------------------------------------------7分
解法3:∵ ,---------------------------------------------------------------1分
,---------------------------------------------------------------1分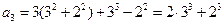 ,--------------------------------------------------------2分
,--------------------------------------------------------2分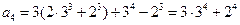 .----------------------------------------------------3分
.----------------------------------------------------3分
由此可猜想出数列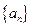 的通项公式为
的通项公式为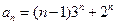 .---------------------------------------4分
.---------------------------------------4分
以下用数学归纳法证明.
①当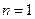 时,
时,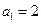 ,等式成立.
,等式成立.
②假设当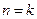 (
(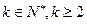 )时等式成立,即
)时等式成立,即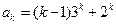 ,
,
那么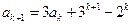
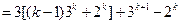
 .----------------------------------------------------------------------6分
.----------------------------------------------------------------------6分
这就是说,当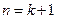 时等式也成立.根据①和②可知,等式
时等式也成立.根据①和②可知,等式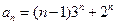 对任何
对任何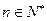 都成立.--------------------------------------------------------------------------------------------------------7分
都成立.--------------------------------------------------------------------------------------------------------7分
(2)令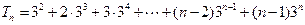 ,--------------------①--------------8分
,--------------------①--------------8分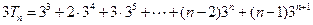 -----------------②------9分
-----------------②------9分
①式减去②式得: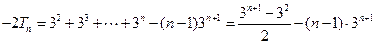 ,-----------------10分
,-----------------10分
∴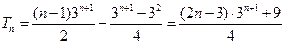 .--------------------------------12分
.--------------------------------12分
∴数列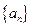 的前
的前 项和
项和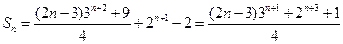 .------14分
.------14分
解析

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案 中,已知圆
中,已知圆 ,
, .
.
 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 是以1为半径,圆心在圆
是以1为半径,圆心在圆 :
: 上移动的动圆 ,若圆
上移动的动圆 ,若圆 分别作圆
分别作圆 的两条切线
的两条切线 ,切点为
,切点为 ,求
,求 的取值范围 ;
的取值范围 ; 同时平分圆
同时平分圆 的周长、圆
的周长、圆 中,角
中,角 、
、 、
、 所对应的边分别为
所对应的边分别为 、
、 、
、 ,且满足
,且满足
 ,求实数
,求实数 的值。
的值。 ,求
,求 的值.
的值. 的正方体
的正方体 中,
中, 是线段
是线段 的中点,底面ABCD的中心是F.
的中点,底面ABCD的中心是F. ^
^ ;
;  ;
;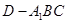 的体积。
的体积。
 的左、右焦点分别为F1、F2.F2也是抛物线C2:
的左、右焦点分别为F1、F2.F2也是抛物线C2: 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且 .
. ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若 ·
· =0,求直线l的方程.
=0,求直线l的方程.