题目内容
设a,b,c都是正数,求证:
(1)(a+b+c) ≥9;
≥9;
(2)(a+b+c) ≥
≥ .
.
(1)(a+b+c)
 ≥9;
≥9;(2)(a+b+c)
 ≥
≥ .
.证明略
证明 (1)∵a,b,c都是正数,
∴a+b+c≥3 ,
, +
+ +
+ ≥3
≥3 .
.
∴(a+b+c) ≥9,
≥9,
当且仅当a=b=c时,等号成立.
(2)∵(a+b)+(b+c)+(c+a)
≥3 ,
,
又 ≥
≥ ,
,
∴(a+b+c) ≥
≥ ,
,
当且仅当a=b=c时,等号成立.
∴a+b+c≥3
 ,
, +
+ +
+ ≥3
≥3 .
.∴(a+b+c)
 ≥9,
≥9,当且仅当a=b=c时,等号成立.
(2)∵(a+b)+(b+c)+(c+a)
≥3
 ,
,又
 ≥
≥ ,
,∴(a+b+c)
 ≥
≥ ,
,当且仅当a=b=c时,等号成立.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 , 求证:
, 求证: .
. ,求证:
,求证: .
.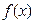 ,
,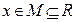 .若
.若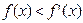 对定义域内的
对定义域内的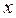 恒成立,则称函数
恒成立,则称函数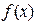 为
为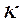 函数.(1)请举出一个定义域为
函数.(1)请举出一个定义域为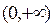 的
的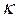 函数,并说明理由;(2)对于定义域为
函数,并说明理由;(2)对于定义域为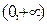 的
的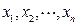 ,均有
,均有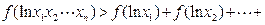
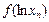 ;
;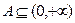 的
的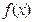 ,求证:
,求证: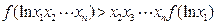 .
.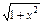 ,a≠b,
,a≠b, <miA
<miA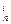

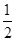 +
+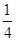 +…+
+…+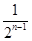 >
>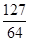 (n∈N*)成立,其初始值至少应取( )
(n∈N*)成立,其初始值至少应取( ) 且
且 ,
, 为大于1的自然数,
为大于1的自然数,