题目内容
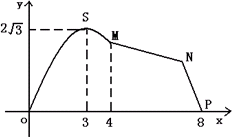
如图,某市拟在长为8 km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数![]() 的图象,且图象的最高点为
的图象,且图象的最高点为![]() ;赛道的后一部分为折线段MNP.为保证参赛运动员的安全,限定∠MNP=120°.
;赛道的后一部分为折线段MNP.为保证参赛运动员的安全,限定∠MNP=120°.
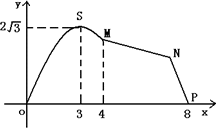
(1)求A,ω的值和M,P两点间的距离;
(2)应如何设计,才能使折线段线段MNP最长?
答案:
解析:
解析:
|
(Ⅰ)依题意,有 又 (Ⅱ)解法一在△MNP中∠MNP=120°,MP=5,设∠PMN= 由正弦定理得 故 解法二:在△MNP中,∠MNP=120°,MP=5, 由余弦定理得 故 当且仅当 |

练习册系列答案
相关题目
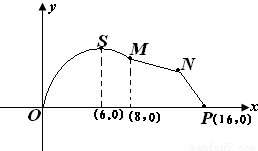
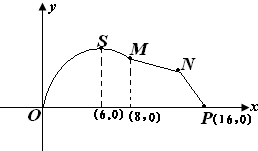 如图,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数y=Asinωx(A>0,ω>0,x∈[0,8]的图象,且图象的最高点为S(6,4
如图,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数y=Asinωx(A>0,ω>0,x∈[0,8]的图象,且图象的最高点为S(6,4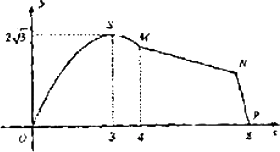
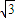 ).赛道的后一段为折线段MNP,为保证参赛队员的安全,限定∠MNP=120°.
).赛道的后一段为折线段MNP,为保证参赛队员的安全,限定∠MNP=120°.