题目内容
当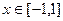 时,
时,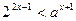 恒成立,求
恒成立,求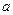 的范围
的范围
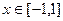 时,
时,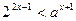 恒成立,求
恒成立,求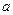 的范围
的范围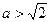
解法一:显然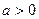 且
且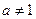 ,两边取常用对数得
,两边取常用对数得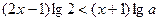
当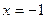 时,显然对任意的
时,显然对任意的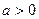 都成立
都成立
当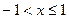 时,可化为
时,可化为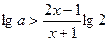

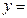
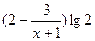 在
在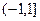 单调增,故当
单调增,故当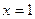 时,
时,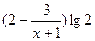 有最大值
有最大值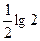
所以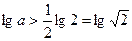 ,所以
,所以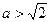
解法二:显然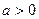 且
且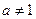 ,
,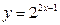 过
过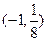 ,
,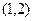 ,
,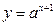 过
过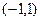
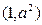
由图像可知只有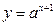 单调增时才能满足题意,所以
单调增时才能满足题意,所以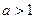
且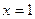 时,
时,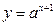 的图像应该在
的图像应该在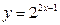 上方,所以
上方,所以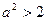 ,所以
,所以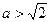
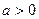 且
且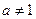 ,两边取常用对数得
,两边取常用对数得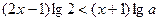
当
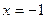 时,显然对任意的
时,显然对任意的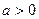 都成立
都成立当
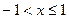 时,可化为
时,可化为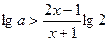

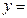
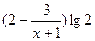 在
在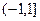 单调增,故当
单调增,故当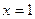 时,
时,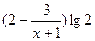 有最大值
有最大值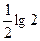
所以
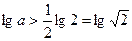 ,所以
,所以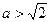
解法二:显然
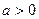 且
且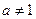 ,
,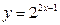 过
过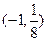 ,
,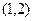 ,
,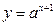 过
过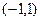
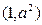
由图像可知只有
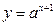 单调增时才能满足题意,所以
单调增时才能满足题意,所以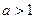
且
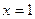 时,
时,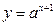 的图像应该在
的图像应该在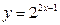 上方,所以
上方,所以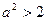 ,所以
,所以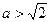

练习册系列答案
相关题目
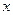 的不等式:
的不等式: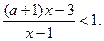
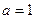 时,求该不等式的解集; (2)当
时,求该不等式的解集; (2)当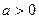 时,求该不等式的解集.
时,求该不等式的解集. 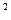 -3x+1>ax
-3x+1>ax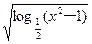 的定义域以及单调递增区间。
的定义域以及单调递增区间。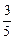 ,1]
,1]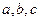 为非零实数,则
为非零实数,则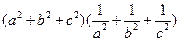 最小值为( ) .
最小值为( ) .
 等式
等式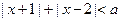 无实数解, 命题
无实数解, 命题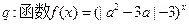 是R上的增函数,若p或q为真命题,p且q为假命题,求实数a的取值范围。
是R上的增函数,若p或q为真命题,p且q为假命题,求实数a的取值范围。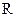 上的偶函数
上的偶函数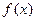 满足
满足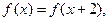 当
当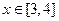 时,
时,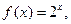 则下列不等式中
则下列不等式中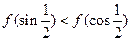
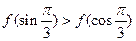
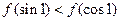

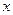 、
、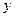 满足
满足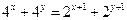 ,则
,则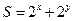 的取值范围是 .
的取值范围是 .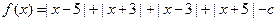 ,若存在正常数
,若存在正常数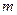 ,使
,使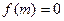 ,则不等式
,则不等式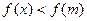 的解集是_________。
的解集是_________。