题目内容
(本小题满分12分)
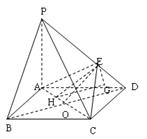
如图所示, 四棱锥P-ABCD的底面是边长为1的正方形,PA^CD,PA = 1, PD=,E为PD上一点,PE = 2ED.
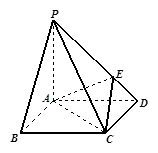
(Ⅰ)求证:PA^平面ABCD;
(Ⅱ)求二面角D-AC-E的余弦值;
(Ⅲ)在侧棱PC上是否存在一点F,使得BF // 平面AEC?若存在,指出F点的位置,并证明;若不存在,说明理由.
如图所示, 四棱锥P-ABCD的底面是边长为1的正方形,PA^CD,PA = 1, PD=,E为PD上一点,PE = 2ED.
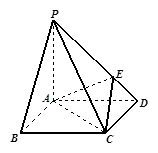
(Ⅰ)求证:PA^平面ABCD;
(Ⅱ)求二面角D-AC-E的余弦值;
(Ⅲ)在侧棱PC上是否存在一点F,使得BF // 平面AEC?若存在,指出F点的位置,并证明;若不存在,说明理由.
(Ⅰ) 见解析;
(Ⅱ)二面角D—AC―E的平面角的余弦值为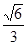 ;
;
(Ⅲ)存在PC的中点F, 使得BF//平面AEC.
(Ⅱ)二面角D—AC―E的平面角的余弦值为
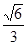 ;
;(Ⅲ)存在PC的中点F, 使得BF//平面AEC.
本试题主要是考查了线面的垂直的证明以及二面角的求解,以及线面平行的判定定理的综合运用
(1)根据已知结合勾股定理和线面垂直的判定定理得到。
(2)建立空间直角坐标系,然后设出点的坐标和向量的坐标,借助于向量的数量积的性质,表示向量的夹角,得到二面角的平面角的求解。
(3)假设存在点PC的中点F, 使得BF//平面AEC.,那个根据假设推理论证,得到结论。
解:(Ⅰ) PA =" PD" =" 1" ,PD =" 2" ,
PA =" PD" =" 1" ,PD =" 2" ,
 PA2 + AD2 = PD2, 即:PA ^ AD ---2分
PA2 + AD2 = PD2, 即:PA ^ AD ---2分
又PA ^ CD , AD , CD 相交于点D,
 PA ^平面ABCD -------4分
PA ^平面ABCD -------4分
(Ⅱ)过E作EG//PA 交AD于G,
从而EG ^平面ABCD,
且AG =" 2GD" , EG = PA = , ------5分
连接BD交AC于O, 过G作GH//OD ,交AC于H,
连接EH. GH ^ AC ,
GH ^ AC , 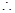 EH ^ AC ,
EH ^ AC ,
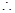 Ð EHG为二面角D—AC―E的平面角. -----6分
Ð EHG为二面角D—AC―E的平面角. -----6分
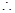 tanÐEHG = = .
tanÐEHG = = .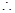 二面角D—AC―E的平面角的余弦值为
二面角D—AC―E的平面角的余弦值为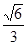 -------7分
-------7分
(Ⅲ)以AB , AD , PA为x轴、y轴、z轴建立空间直角坐标系.
则A(0 ,0, 0),B(1,0,0) ,C(1,1,0),P(0,0,1),E(0 , ,),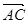 = (1,1,0),
= (1,1,0),
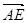 = (0 , , )
= (0 , , )
设平面AEC的法向量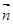 = (x, y,z) , 则
= (x, y,z) , 则
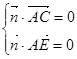 ,即:
,即: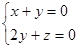 , 令y =" 1" ,
, 令y =" 1" ,
则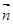 = (- 1,1, - 2 ) -------------10分
= (- 1,1, - 2 ) -------------10分
假设侧棱PC上存在一点F, 且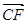 =
= 
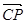 ,
,
(0 £ £ 1), 使得:BF//平面AEC, 则
£ 1), 使得:BF//平面AEC, 则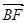 ×
×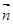 = 0.
= 0.
又因为: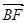 =
= 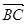 +
+ 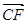 = (0 ,1,0)+ (-
= (0 ,1,0)+ (- ,-
,- ,
, )= (-
)= (- ,1-
,1- ,
, ),
),
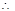
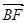 ×
× =
= + 1-
+ 1-  - 2
- 2 =" 0" ,
=" 0" , 
 = ,
= ,
所以存在PC的中点F, 使得BF//平面AEC. ----------------12分
(1)根据已知结合勾股定理和线面垂直的判定定理得到。
(2)建立空间直角坐标系,然后设出点的坐标和向量的坐标,借助于向量的数量积的性质,表示向量的夹角,得到二面角的平面角的求解。
(3)假设存在点PC的中点F, 使得BF//平面AEC.,那个根据假设推理论证,得到结论。
解:(Ⅰ)
 PA =" PD" =" 1" ,PD =" 2" ,
PA =" PD" =" 1" ,PD =" 2" ,  PA2 + AD2 = PD2, 即:PA ^ AD ---2分
PA2 + AD2 = PD2, 即:PA ^ AD ---2分又PA ^ CD , AD , CD 相交于点D,
 PA ^平面ABCD -------4分
PA ^平面ABCD -------4分(Ⅱ)过E作EG//PA 交AD于G,
从而EG ^平面ABCD,
且AG =" 2GD" , EG = PA = , ------5分
连接BD交AC于O, 过G作GH//OD ,交AC于H,

连接EH.
 GH ^ AC ,
GH ^ AC ,  EH ^ AC ,
EH ^ AC ,  Ð EHG为二面角D—AC―E的平面角. -----6分
Ð EHG为二面角D—AC―E的平面角. -----6分 tanÐEHG = = .
tanÐEHG = = . 二面角D—AC―E的平面角的余弦值为
二面角D—AC―E的平面角的余弦值为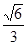 -------7分
-------7分(Ⅲ)以AB , AD , PA为x轴、y轴、z轴建立空间直角坐标系.
则A(0 ,0, 0),B(1,0,0) ,C(1,1,0),P(0,0,1),E(0 , ,),
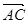 = (1,1,0),
= (1,1,0), 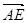 = (0 , , )
= (0 , , ) 设平面AEC的法向量
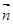 = (x, y,z) , 则
= (x, y,z) , 则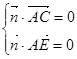 ,即:
,即: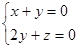 , 令y =" 1" ,
, 令y =" 1" , 则
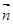 = (- 1,1, - 2 ) -------------10分
= (- 1,1, - 2 ) -------------10分假设侧棱PC上存在一点F, 且
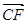 =
= 
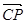 ,
, (0 £
 £ 1), 使得:BF//平面AEC, 则
£ 1), 使得:BF//平面AEC, 则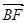 ×
×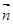 = 0.
= 0.又因为:
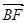 =
= 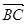 +
+ 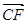 = (0 ,1,0)+ (-
= (0 ,1,0)+ (- ,-
,- ,
, )= (-
)= (- ,1-
,1- ,
, ),
),
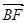 ×
× =
= + 1-
+ 1-  - 2
- 2 =" 0" ,
=" 0" , 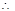
 = ,
= ,所以存在PC的中点F, 使得BF//平面AEC. ----------------12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
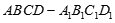 ,
,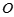 是底
是底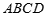 对角线的交点.
对角线的交点.
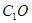 ∥面
∥面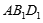 ;
;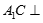 面
面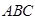
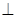 平面
平面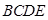 ,
, 与
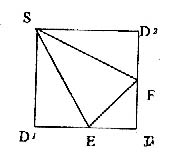
与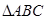 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形,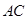 //
//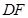 ,四边形
,四边形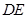 //
//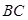 ,
,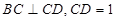 ,点
,点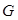 为
为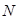 为
为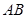 中点,
中点,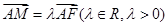 ,
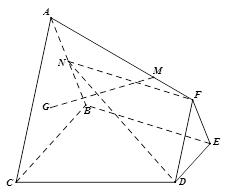
,
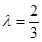 时,求证:
时,求证: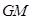 //平面
//平面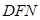
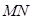 与
与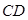 所成角为
所成角为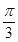 ,试求二面角
,试求二面角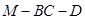 的余弦值.
的余弦值.
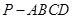 中,底面
中,底面 是矩形,
是矩形,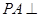 平面
平面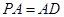 ,
,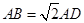 ,
,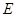 是线段
是线段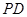 上的点,
上的点,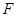 是线段
是线段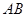 上的点,且
上的点,且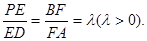

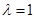 时,证明
时,证明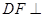 平面
平面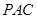 ;
;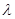 ,使异面直线
,使异面直线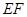 与
与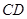 所成的角为
所成的角为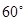 ?若存在,试求出
?若存在,试求出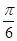 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD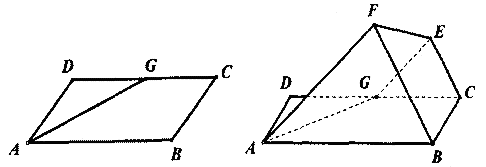
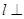 平面
平面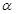 ,直线
,直线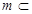 平面
平面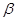 ,则下列四个命题中正确的是 ( )
,则下列四个命题中正确的是 ( )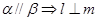 ②
②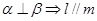 ;③
;③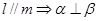 ;④
;④