题目内容
已知椭圆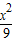
+
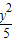=1的左右焦点为F1、F2，P为椭圆上一点，O是坐标原点，M是PF1的中点，若|PF1|=4，则|OM|= ．
【答案】分析：由椭圆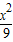
+
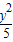=1的左右焦点为F1、F2，P为椭圆上一点，|PF1|=4，知|PF2|=2，再由M是PF1的中点，由三角形中位线定理能求出|OM|的长．
解答：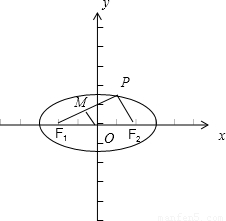
解：∵椭圆
+
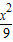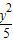=1的左右焦点为F1、F2，
P为椭圆上一点，|PF1|=4，
∴|PF2|=2×3-4=2，
∵M是PF1的中点，O是F1F2中点，
∴|OM|=
|PF2|=1．
故答案为：1．
点评：本题考查椭圆中线段长的求法，是基础题．解题时要认真审题，注意椭圆定义和三角形中位线性质的灵活运用．
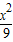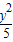+=1的左右焦点为F1、F2，P为椭圆上一点，|PF1|=4，知|PF2|=2，再由M是PF1的中点，由三角形中位线定理能求出|OM|的长．解答：
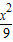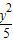解：∵椭圆+=1的左右焦点为F1、F2，P为椭圆上一点，|PF1|=4，
∴|PF2|=2×3-4=2，
∵M是PF1的中点，O是F1F2中点，
∴|OM|=
|PF2|=1．故答案为：1．
点评：本题考查椭圆中线段长的求法，是基础题．解题时要认真审题，注意椭圆定义和三角形中位线性质的灵活运用．
练习册系列答案
相关题目
+
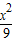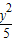=1的左右焦点为F1、F2，P为椭圆上一点，O是坐标原点，M是PF1的中点，若|PF1|=4，则|OM|= ．
+
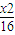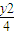=1的左右焦点分别为F1与F2，点P在直线l：x-
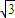y+8+2
=0上．当∠F1PF2取最大值时，
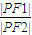的比值为 ．
+
=1的左右焦点分别为F1与F2，点P在直线l：x-
y+8+2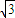
=0上．当∠F1PF2取最大值时，
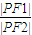的比值为 ．