题目内容
己知:函数f(x)=x3+ax2+bx+c,在(-∝,-1),(2,+∝)上单凋递增,在(一1,2)上单调递减,不等式f(x)>x2-4x+5的解集为(4,+∝).(I)求函数f(x)的解析式;
(II)若函数h(x)=
 ,求h(x)的单调区间.
,求h(x)的单调区间.
【答案】分析:(I)先根据函数的单调性可知f'(x)=3x2+2ax+b=0有两个根-1,2,求出a和b,然后根据不等式f(x)>x2-4x+5的解集为(4,+∝)求出c,从而求出函数f(x)的解析式;
(II)先求出函数h(x)的解析式,然后讨论m的取值范围,根据导函数的符号与函数单调性的关系求出相应的单调区间,从而求出所求.
解答:解:(Ⅰ)在(-∝,-1),(2,+∝)上单凋递增,在(一1,2)上单调递减,
∴f'(x)=3x2+2ax+b=0有两个根-1,2
利用根与系数的关系可知a= ,b=-6
,b=-6
∴f(x)=x3 x2-6x+c,
x2-6x+c,
∵不等式f(x)>x2-4x+5的解集为(4,+∝).
∴c=-11
∴f(x)=x3 x2-6x-11,
x2-6x-11,
(Ⅱ)f'(x)=3x2-3x-6=3(x+1)(x-2),
∴h(x)= =(x+1)-(m+1)ln(x+m)(x>-m且,x≠2)
=(x+1)-(m+1)ln(x+m)(x>-m且,x≠2)
当m≤-2时,-m≥2,定义域:(-m,+∞),
h'(x)>0恒成立,h(x)在(-m,+∞)上单增;
当-2<m≤-1时,定义域:(-m,2)∪(2,+∞)
h'(x)恒成立,h(x)在(-m,2)与(2,+∞)上单增;
当m>-1时,-m<1,定义域:(-m,2)∪(2,+∞)
由 h'(x)>0得x>1,由h'(x)<0 得x<1.
故在(1,2),(2,+∞)上单增;在(-m,1)上单减,
综上所述,当m≤-2时,h(x)在(-m,+∞)上单增;
当-2<m≤-1时,h(x)在(-m,2)与(2,+∞)上单增;
当m>-1时,在(1,2),(2,+∞)上单增;在(-m,1)单减.
点评:本题主要考查了函数的单调性与导数的关系,函数与方程的综合运用,是一道综合题,同时考查了计算能力,转化与划归的思想,属于中档题.
(II)先求出函数h(x)的解析式,然后讨论m的取值范围,根据导函数的符号与函数单调性的关系求出相应的单调区间,从而求出所求.
解答:解:(Ⅰ)在(-∝,-1),(2,+∝)上单凋递增,在(一1,2)上单调递减,
∴f'(x)=3x2+2ax+b=0有两个根-1,2
利用根与系数的关系可知a=
 ,b=-6
,b=-6∴f(x)=x3
 x2-6x+c,
x2-6x+c,∵不等式f(x)>x2-4x+5的解集为(4,+∝).
∴c=-11
∴f(x)=x3
 x2-6x-11,
x2-6x-11,(Ⅱ)f'(x)=3x2-3x-6=3(x+1)(x-2),
∴h(x)=
 =(x+1)-(m+1)ln(x+m)(x>-m且,x≠2)
=(x+1)-(m+1)ln(x+m)(x>-m且,x≠2)当m≤-2时,-m≥2,定义域:(-m,+∞),
h'(x)>0恒成立,h(x)在(-m,+∞)上单增;
当-2<m≤-1时,定义域:(-m,2)∪(2,+∞)
h'(x)恒成立,h(x)在(-m,2)与(2,+∞)上单增;
当m>-1时,-m<1,定义域:(-m,2)∪(2,+∞)
由 h'(x)>0得x>1,由h'(x)<0 得x<1.
故在(1,2),(2,+∞)上单增;在(-m,1)上单减,
综上所述,当m≤-2时,h(x)在(-m,+∞)上单增;
当-2<m≤-1时,h(x)在(-m,2)与(2,+∞)上单增;
当m>-1时,在(1,2),(2,+∞)上单增;在(-m,1)单减.
点评:本题主要考查了函数的单调性与导数的关系,函数与方程的综合运用,是一道综合题,同时考查了计算能力,转化与划归的思想,属于中档题.

练习册系列答案
相关题目
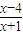 (x≠-1)的反函数是f-1(x).设数列{an}的前n项和为Sn,对任意的正整数都有an=
(x≠-1)的反函数是f-1(x).设数列{an}的前n项和为Sn,对任意的正整数都有an=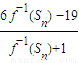 成立,且bn=f-1(an)•
成立,且bn=f-1(an)• ;
;