题目内容
(本小题满分12分)
已知椭圆
 的离心率为
的离心率为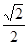 ,点
,点 是椭圆上的一点,且点
是椭圆上的一点,且点 到椭圆
到椭圆 的两焦点的距离之和为4,
的两焦点的距离之和为4,
(1)求椭圆 的方程;
的方程;
(2)过点 作直线
作直线 与椭圆
与椭圆 交于
交于 两点,
两点, 是坐标原点,设
是坐标原点,设 ,是否存在这样的直线
,是否存在这样的直线 ,使四边形
,使四边形 的对角线长相等?若存在,求出
的对角线长相等?若存在,求出 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
【答案】
(1)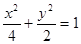
(2)不存在,证明略。
【解析】
(1)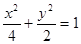 …………….4分
…………….4分
(2)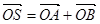 ,所以四边形
,所以四边形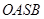 为平行四边形
为平行四边形
假设存在直线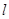 ,使
,使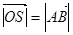
所以四边形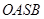 为矩形,
为矩形,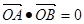
设直线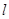 的斜率不存在,则直线的方程为
的斜率不存在,则直线的方程为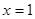
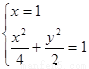 则
则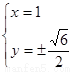 所以
所以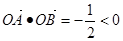 舍
舍
若直线的斜率存在,设直线的方程为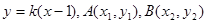
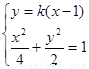 故
故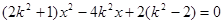
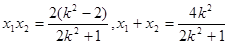
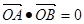 所以
所以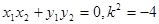 不存在
不存在
综上,满足条件的直线不存在。………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目