Question

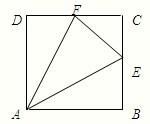如图，正方形ABCD中，E，F分别为BC，CD的中点，设∠EAF=θ，则cosθ=

 

．

Answer 1

分析：根据直角三角形中的边角关系可得 tan∠EAB 和tan∠FAD，可求出tan（∠EAB+∠FAD ），进而求得 tanθ=
tan[

π

2

-（∠EAB+∠FAD ）]的值，利用同角三角函数的基本关系求出 cosθ 的值．

解答：解：设正方形ABCD的边长等于1，根据直角三角形中的边角关系可得 tan∠EAB=

EB

AB

=

1

2

，
tan∠FAD=

DF

AD

=

1

2

，∴tan（∠EAB+∠FAD ）=

tan∠EAB +tan∠ FAD

1- tan∠EAB •tan∠ FAD

=

4

3

，
∴tanθ=tan[

π

2

-（∠EAB+∠FAD ）]=cot（∠EAB+∠FAD ）=

3

4

，
故 cosθ=

4

5

，
故答案为

4

5

．

点评：本题考查直角三角形中的边角关系，同角三角函数的基本关系，两角和的正切公式的应用，求出tanθ=

3

4

，
是解题的关键，属于中档题．