题目内容
设a、b、c均为实数，且a=x2-2y+
,b=y2-2x+
，c=z2-2x+
.求证：a、b、c中至少有一个大于0.
证明：假设a、b、c都不大于0，即a≤0,b≤0,c≤0,则a+b+c≤0.
则a+b+c=x2-2y++y2-2z++z2-2x+=(x-1)2+(y-1)2+(z-1)2+π-3＞0,
∴a+b+c＞0.
与a+b+c≤0矛盾.因此，a、b、c中至少有一个大于0.
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
+
+
≥
+
+
．
+
+
≥
+
+
．
+
+
≥
+
+
．
+
+
≥
+
+
．
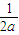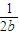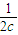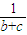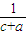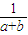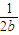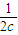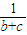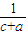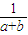