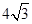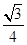题目内容
如图,边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点△AED,△EBF,△FCD分别沿DE,EF,FD折起,使A,B,C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为
A. | B. | C. | D. |
B
解析试题分析:因为DA⊥Rt△AEF,所以四面体A′EFD的外接球,与以A′、E、F、D所确定的长方体的外接球是同一外接球,所以其外接球半径r=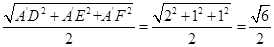 .
.
考点:三棱锥的外接球问题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知一个四面体有五条棱长都等于2,则该四面体的体积最大值为( )
A. | B.1 | C. | D.2 |
一个几何体的三视图如图所示,则该机合体的体积为( )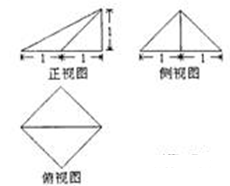
A.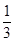 | B.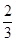 | C.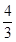 | D.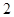 |
一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是( )
| A.球, | B.三棱锥, | C.正方体, | D.圆柱 |
正三棱锥的高和底面边长都等于6,则其外接球的表面积为( )
A. | B. | C. | D. |
平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为 ,则此球的体积为( )
,则此球的体积为( )
A. π π | B.4 π π |
C.4 π π | D.6 π π |
平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为 ,则此球的体积为( )
,则此球的体积为( )
A. π π | B.4 π π | C.4 π π | D.6 π π |
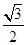 ,且一个内角为
,且一个内角为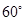 的菱形,俯视图为正方形,那么这个几何体的表面积为( )
的菱形,俯视图为正方形,那么这个几何体的表面积为( )