题目内容
椭圆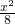 +
+ =1和双曲线
=1和双曲线 -
- =1的公共焦点为F1,F2,P是两曲线的一个交点,那么∠F1PF2=________.
=1的公共焦点为F1,F2,P是两曲线的一个交点,那么∠F1PF2=________.
90°
分析:根据椭圆和双曲线的定义可得PF1+PF2=2a=4 ,PF1-PF2=2a′=4,解得PF1和PF2 的值,三角形F1PF2 中,由余弦定理可得4c2=PF12+PF22-2PF1•PF2cos∠F1PF2,解方程求得cos∠F1PF2的值,进而可得答案.
,PF1-PF2=2a′=4,解得PF1和PF2 的值,三角形F1PF2 中,由余弦定理可得4c2=PF12+PF22-2PF1•PF2cos∠F1PF2,解方程求得cos∠F1PF2的值,进而可得答案.
解答:由椭圆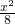 +
+ =1 可得,a=2
=1 可得,a=2 ,c=
,c= ,再根据椭圆和双曲线的定义可得
,再根据椭圆和双曲线的定义可得
PF1+PF2=2a=4 ,PF1-PF2=2a′=4,解得 PF1=
,PF1-PF2=2a′=4,解得 PF1=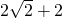 ,PF2=
,PF2=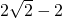 .
.
三角形F1PF2 中,由余弦定理可得4c2=PF12+PF22-2PF1•PF2cos∠F1PF2,
解得 cos∠F1PF2=0,
则∠F1PF2=90°,
故答案为90°.
点评:本题考查直线和圆锥曲线的位置关系,椭圆、双曲线的定义和标准方程,以及余弦定理的应用,求出 PF1和PF2的值,是解题的关键.
分析:根据椭圆和双曲线的定义可得PF1+PF2=2a=4
 ,PF1-PF2=2a′=4,解得PF1和PF2 的值,三角形F1PF2 中,由余弦定理可得4c2=PF12+PF22-2PF1•PF2cos∠F1PF2,解方程求得cos∠F1PF2的值,进而可得答案.
,PF1-PF2=2a′=4,解得PF1和PF2 的值,三角形F1PF2 中,由余弦定理可得4c2=PF12+PF22-2PF1•PF2cos∠F1PF2,解方程求得cos∠F1PF2的值,进而可得答案.解答:由椭圆
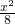 +
+ =1 可得,a=2
=1 可得,a=2 ,c=
,c= ,再根据椭圆和双曲线的定义可得
,再根据椭圆和双曲线的定义可得 PF1+PF2=2a=4
 ,PF1-PF2=2a′=4,解得 PF1=
,PF1-PF2=2a′=4,解得 PF1=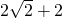 ,PF2=
,PF2=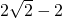 .
.三角形F1PF2 中,由余弦定理可得4c2=PF12+PF22-2PF1•PF2cos∠F1PF2,
解得 cos∠F1PF2=0,
则∠F1PF2=90°,
故答案为90°.
点评:本题考查直线和圆锥曲线的位置关系,椭圆、双曲线的定义和标准方程,以及余弦定理的应用,求出 PF1和PF2的值,是解题的关键.

练习册系列答案
相关题目