Question

在△ABC中，a，b，c分别是三内角A、B、C的对边，且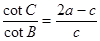，a²＋b²＝c²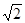＋ab，求A．

 

Answer 1

【答案】

 

【解析】

试题分析：∵　a²＋b²＝c²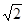＋ab

　　∴　

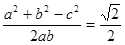
　　∴　cosC＝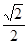

　　∴　C＝45°

　　由正弦定理可得

　　

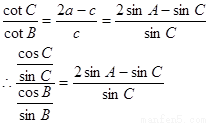
　　∴　sinBcosC＝2sinAcosB-sinCcosB

　　∴　sinBcosC＋sinCcosB＝2sinAcosB

　　∴　sin(B＋C)＝2sinAcosB

　　∴　sinA＝2sinAcosB

　　∵　sinA≠0

　　∴　cosB＝

　　∴　B＝60°，∴　A＝180°-45°-60°＝75°

考点：本题主要考查正弦定理、余弦定理、两角和与差的三角函数。

点评：在三角形中，利用正弦定理、余弦定理确定边角关系，是常见题型。本题与三角恒等变换相结合，考查了运用知识的灵活性。