题目内容
(本题14分).在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, .以
.以 的中点
的中点 为球心、
为球心、 为直径的球面交
为直径的球面交 于点
于点 ,交
,交 于点
于点 .
.
(1)求直线 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
(2)求点 到平面
到平面 的距离.
的距离.
【答案】
(1)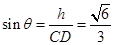
(2)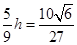
【解析】解法一: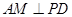 ,又
,又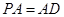 ,则
,则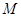 是
是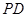 的中点,故
的中点,故
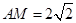 ,
,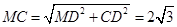 ,
,
则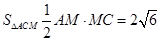 ,
,
设D到平面ACM的距离为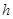 ,由
,由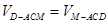 ,有
,有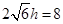 ,可求得
,可求得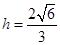 ,
,
设直线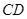 与平面
与平面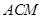 所成的角为
所成的角为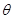 ,则
,则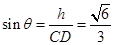 .
.
(2)可求得PC=6.因为AN⊥NC,由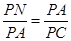 ,得PN
,得PN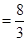 .
.
所以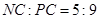 .故N点到平面ACM的距离等于P点到平面ACM距离的
.故N点到平面ACM的距离等于P点到平面ACM距离的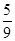 .
.
又因为M是PD的中点,则P、D到平面ACM的距离相等,由⑵可知所求距离为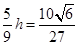 .
.
解法二:
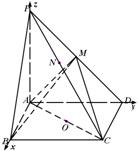 (1)如图所示,建立空间直角坐标系,则
(1)如图所示,建立空间直角坐标系,则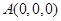 ,
, ,
,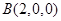 ,
,
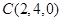 ,
,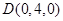 ,
,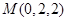 ;
;
设平面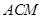 的一个法向量
的一个法向量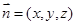 ,由
,由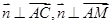 ,
,
可得: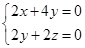 ,令
,令 ,则
,则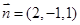 .
.
设所求角为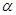 ,则
,则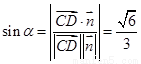 .
.
(2)由条件可得,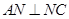 .在
.在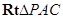 中,
中,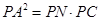 ,
,
所以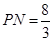 ,则
,则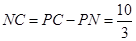 ,
,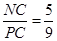 ,
,
所以所求距离等于点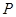 到平面
到平面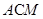 距离的
距离的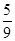 ,
,
设点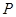 到平面
到平面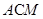 距离为
距离为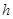 ,则
,则 ,故所求距离为
,故所求距离为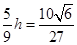 .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, .以
.以 的中点
的中点 为球心、
为球心、 于点
于点 ,交
,交 于点
于点 .
. 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;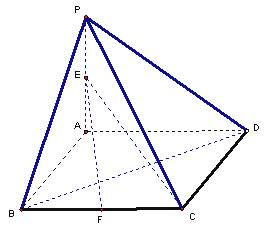 如图,在四棱锥
如图,在四棱锥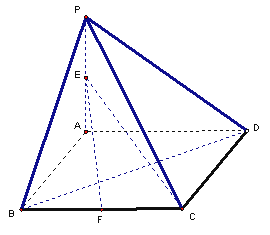 如图,在四棱锥
如图,在四棱锥 (1)求直线
(1)求直线