题目内容
 5、在直四棱柱ABCD-A1B1C1D1中,当底面四边形ABCD满足条件
5、在直四棱柱ABCD-A1B1C1D1中,当底面四边形ABCD满足条件AC⊥BD或四边形ABCD为菱形
时,有A1C⊥B1D1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情况)分析:由假设A1C⊥B1D1,结合直四棱柱的性质及线面垂直的判定和性质定理,我们易得到A1C1⊥B1D1,即AC⊥BD,又由菱形的几何特征可判断出四边形ABCD为菱形,又由本题为开放型题目上,故答案可以不唯一.
解答:解:若A1C⊥B1D1,由四棱柱ABCD-A1B1C1D1为直四棱柱
AA1⊥B1D1,易得B1D1⊥平面AA1BB1,
则A1C1⊥B1D1,即AC⊥BD
则四边形ABCD为菱形
故答案为:AC⊥BD或四边形ABCD为菱形
AA1⊥B1D1,易得B1D1⊥平面AA1BB1,
则A1C1⊥B1D1,即AC⊥BD
则四边形ABCD为菱形
故答案为:AC⊥BD或四边形ABCD为菱形
点评:本题考查的知识点是空间中直线与直线之间的位置关系,三垂线定理,线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.

练习册系列答案
相关题目
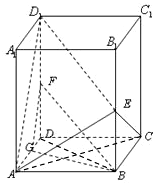 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.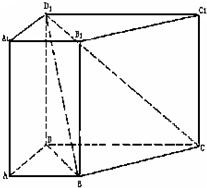 在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.
在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.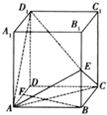 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点. 如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=
如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE= 在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.
在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.