题目内容
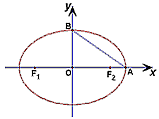
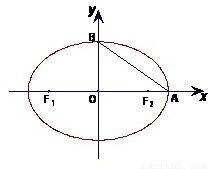
如图,椭圆的两顶点为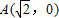 ,B(0,1),该椭圆的左右焦点分别是F1,F2.
,B(0,1),该椭圆的左右焦点分别是F1,F2.(1)在线段AB上是否存在点C,使得CF1⊥CF2?若存在,请求出点C的坐标;若不存在,请说明理由.
(2)设过F1的直线交椭圆于P,Q两点,求△PQF2面积的最大值.
【答案】分析:(1)根据椭圆的方程求得a和b,c,进而求得焦点的坐标,表示出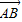 假设存在点C,使CF1⊥CF2,求得|OC|,令
假设存在点C,使CF1⊥CF2,求得|OC|,令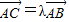 ,利用
,利用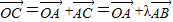 求得λ的方程,解方程求得λ.
求得λ的方程,解方程求得λ.
(2)设出P,Q的坐标,通过焦半径公式求得|PQ|的表达式,先看PQ⊥x轴时,则可求得x1=x2=-1进而求得△PQF2面积;再看PQ与x轴不垂直时,设出PQ的方程,由点到直线的距离公式可得点F2到PQ的距离表示出△PQF2面积的表达式,利用基本不等式求得△PQF2面积的范围,最后综合推断出△PQF2面积的最大值.
解答: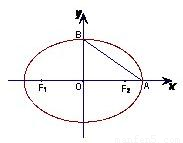 解:由已知可得椭圆的方程为
解:由已知可得椭圆的方程为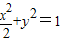 ,
,
且有: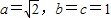 ,F1(-1,0),
,F1(-1,0),
F2(1,0),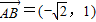 .
.
(1)假设存在点C,使得CF1⊥CF2,
则: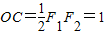 ,
,
令 (λ∈[0,1]),
(λ∈[0,1]),
而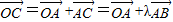 =
=
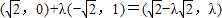 ,
,
故有: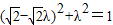 ,解得λ=1或
,解得λ=1或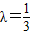 .
.
所以点C的坐标为C(0,1)或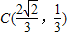 .
.
(2)若设过F1的直线l交椭圆于P(x1,y1),Q(x2,y2),则由焦半径公式可得: ,
,
当PQ⊥x轴时,x1=x2=-1,此时 .
.
当PQ与x轴不垂直时,不妨设直线PQ的方程为y=k(x+1),(k>0),
则由: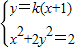 得:(2k2+1)x2+4k2x+2k2-2=0,故
得:(2k2+1)x2+4k2x+2k2-2=0,故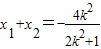 ,
,
于是可得: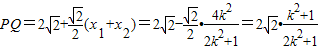 .
.
又由点到直线的距离公式可得点F2到PQ的距离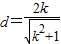 ,
,
故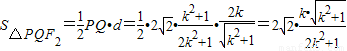 .
.
因为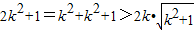 ,
,
所以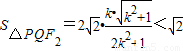 .
.
综上可知,当直线PQ⊥x轴时,△PQF2的面积取到最大值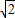 .
.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了运用解析几何的基础知识解决实际问题的能力.
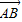 假设存在点C,使CF1⊥CF2,求得|OC|,令
假设存在点C,使CF1⊥CF2,求得|OC|,令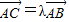 ,利用
,利用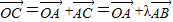 求得λ的方程,解方程求得λ.
求得λ的方程,解方程求得λ.(2)设出P,Q的坐标,通过焦半径公式求得|PQ|的表达式,先看PQ⊥x轴时,则可求得x1=x2=-1进而求得△PQF2面积;再看PQ与x轴不垂直时,设出PQ的方程,由点到直线的距离公式可得点F2到PQ的距离表示出△PQF2面积的表达式,利用基本不等式求得△PQF2面积的范围,最后综合推断出△PQF2面积的最大值.
解答:
 解:由已知可得椭圆的方程为
解:由已知可得椭圆的方程为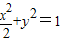 ,
,且有:
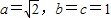 ,F1(-1,0),
,F1(-1,0),F2(1,0),
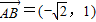 .
.(1)假设存在点C,使得CF1⊥CF2,
则:
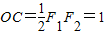 ,
,令
 (λ∈[0,1]),
(λ∈[0,1]),而
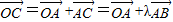 =
=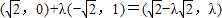 ,
,故有:
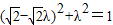 ,解得λ=1或
,解得λ=1或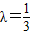 .
.所以点C的坐标为C(0,1)或
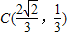 .
.(2)若设过F1的直线l交椭圆于P(x1,y1),Q(x2,y2),则由焦半径公式可得:
 ,
,当PQ⊥x轴时,x1=x2=-1,此时
 .
.当PQ与x轴不垂直时,不妨设直线PQ的方程为y=k(x+1),(k>0),
则由:
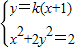 得:(2k2+1)x2+4k2x+2k2-2=0,故
得:(2k2+1)x2+4k2x+2k2-2=0,故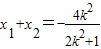 ,
,于是可得:
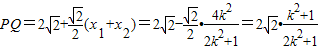 .
.又由点到直线的距离公式可得点F2到PQ的距离
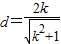 ,
,故
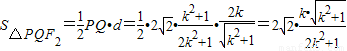 .
.因为
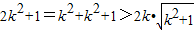 ,
,所以
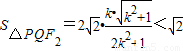 .
.综上可知,当直线PQ⊥x轴时,△PQF2的面积取到最大值
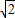 .
.点评:本题主要考查了直线与圆锥曲线的综合问题.考查了运用解析几何的基础知识解决实际问题的能力.

练习册系列答案
相关题目
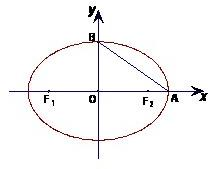 如图,椭圆的两顶点为
如图,椭圆的两顶点为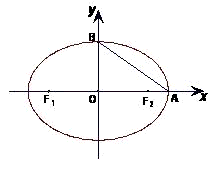 如图,椭圆的两顶点为
如图,椭圆的两顶点为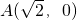 ,B(0,1),该椭圆的左右焦点分别是F1,F2.
,B(0,1),该椭圆的左右焦点分别是F1,F2.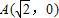 ,B(0,1),该椭圆的左右焦点分别是F1,F2.
,B(0,1),该椭圆的左右焦点分别是F1,F2.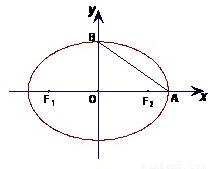
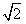 ,0),B(0,1),该椭圆的左右焦点分别是F1,F2。
,0),B(0,1),该椭圆的左右焦点分别是F1,F2。