题目内容
已知椭圆E: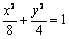 的左焦点为F,左准线
的左焦点为F,左准线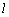 与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.
与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.
(1)求圆C的方程;
(2)若直线FG与直线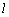 交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
(3)在平面上是否存在一点P,使得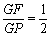 ?若存在,求出点P坐标;若不存在,请说明理由.
?若存在,求出点P坐标;若不存在,请说明理由.
【答案】
(1)由椭圆E: ,得
,得 :
: ,
,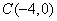 ,
,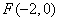 ,
,
又圆C过原点,所以圆C的方程为 .………………………………4分
.………………………………4分
(2)由题意,得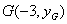 ,代入
,代入 ,得
,得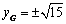 ,
,
所以 的斜率为
的斜率为 ,
, 的方程为
的方程为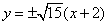 , …………………8分
, …………………8分
(注意:若点G或FG方程只写一种情况扣1分)
所以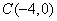 到
到 的距离为
的距离为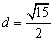 ,直线
,直线 被圆C截得弦长为
被圆C截得弦长为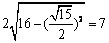 .
.
故直线 被圆C截得弦长为7.…………………………………………………………10分
被圆C截得弦长为7.…………………………………………………………10分
(3)设 ,
,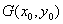 ,则由
,则由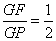 ,得
,得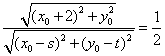 ,
,
整理得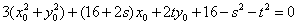 ①,…………………………12分
①,…………………………12分
又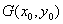 在圆C:
在圆C: 上,所以
上,所以 ②,
②,
②代入①得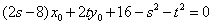 , …………………………14分
, …………………………14分
又由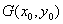 为圆C 上任意一点可知,
为圆C 上任意一点可知,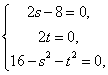 解得
解得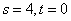 .
.
所以在平面上存在一点P,其坐标为 . …………………………16分
. …………………………16分

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
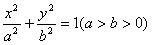 的左焦点F1(
的左焦点F1(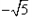 ,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F。
,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F。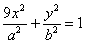 ,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连结MN,试问当k为何值时,直线MN过椭圆G的顶点?
,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连结MN,试问当k为何值时,直线MN过椭圆G的顶点?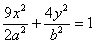 于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB。
于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB。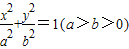 的左顶点为A,左、右焦点分别为F1、F2,且圆C:
的左顶点为A,左、右焦点分别为F1、F2,且圆C: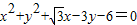 过A,F2两点.
过A,F2两点.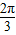 时,证明:点P在一定圆上.
时,证明:点P在一定圆上.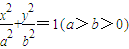 的左焦点
的左焦点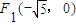 ,若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F.
,若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F.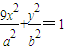 ,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连接MN,试问当k为何值时,直线MN过椭圆G的顶点?
,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连接MN,试问当k为何值时,直线MN过椭圆G的顶点?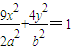 于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC并延长交椭圆W于B,求证:PA⊥PB.
于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC并延长交椭圆W于B,求证:PA⊥PB.