题目内容
已知函数f(x)=kx-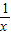 ,且f(1)=1.
,且f(1)=1.(1)求实数k的值;
(2)判断并证明函数在(0,+∞)的单调性;
(3)求f(x)在[2,5]上的值域.
【答案】分析:(1)由f(1)=k-1=1即可求解k
(2)由(1)可求f(x),然后对已知函数求导,结合导数的正负即可判断原函数的单调性
(3)结合f(x)在(0,+∞)单调性即可求解函数在[2,5]上的单调性,进而可求最值
解答:解:(1)∵f(1)=k-1=1
∴k=2
证明:(2)由(1)可得f(x)=2x-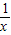
f(x)在(0,+∞)单调递增,证明如下
∵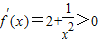 在x>0时恒成立
在x>0时恒成立
∴f(x)在(0,+∞)单调递增
解:(3)∵f(x)在(0,+∞)单调递增,
∴f(x)在[2,5]上单调递增
∴当x=2时函数取得最小值f(2)=4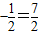 ,当x=5时函数取得最大值f(5)=
,当x=5时函数取得最大值f(5)=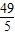
点评:本题主要考查了利用待定系数求解函数 的解析式,函数的单调性的判断与证明及利用单调性求解函数的 最值
(2)由(1)可求f(x),然后对已知函数求导,结合导数的正负即可判断原函数的单调性
(3)结合f(x)在(0,+∞)单调性即可求解函数在[2,5]上的单调性,进而可求最值
解答:解:(1)∵f(1)=k-1=1
∴k=2
证明:(2)由(1)可得f(x)=2x-
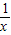
f(x)在(0,+∞)单调递增,证明如下
∵
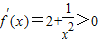 在x>0时恒成立
在x>0时恒成立∴f(x)在(0,+∞)单调递增
解:(3)∵f(x)在(0,+∞)单调递增,
∴f(x)在[2,5]上单调递增
∴当x=2时函数取得最小值f(2)=4
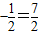 ,当x=5时函数取得最大值f(5)=
,当x=5时函数取得最大值f(5)=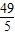
点评:本题主要考查了利用待定系数求解函数 的解析式,函数的单调性的判断与证明及利用单调性求解函数的 最值

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目