题目内容
设函数f(x)= 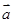 ×
×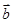 ,其中向量
,其中向量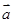 ="(2cosx,1),"
="(2cosx,1),"
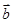 =(cosx,
=(cosx,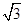 sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和f(x)在[0, p]上的单调递增区间;
(2)当xÎ[0,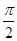 ]时,ô f(x)ô <4恒成立,求实数m的取值范围.
]时,ô f(x)ô <4恒成立,求实数m的取值范围.
【答案】
(1) T=p, [0,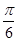 ],[
],[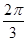 , p] (2) -4<m<1.
, p] (2) -4<m<1.
【解析】
试题分析:(1)f(x)= 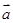 ×
×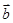 =2cos2x+
=2cos2x+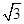 sin2x+m
1分
sin2x+m
1分
=cos2x+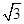 sin2x+m+1=2sin(2x+
sin2x+m+1=2sin(2x+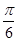 )+m+1
3分
)+m+1
3分
∴f(x)的最小正周期T=p, 4分
在[0, p]上的单调递增区间为[0,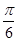 ],[
],[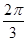 ,p] 6分
,p] 6分
(2)∵当xÎ[0,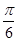 ]时,
]时,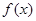 递增,当xÎ[
递增,当xÎ[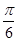 ,
,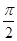 ]时,
]时,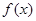 递减,
递减,
∴当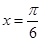 时,
时,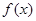 的最大值等于
的最大值等于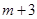 . 8分
. 8分
当x=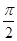 时,
时,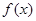 的最小值等于m. 10分
的最小值等于m. 10分
由题设知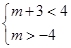 解之得,-4<m<1. 12分
解之得,-4<m<1. 12分
考点:本题考查了三角函数的性质及最值
点评:三角函数最值问题是历年高考重点考查的知识点之一,它不仅与三角自身的常见基础知识如三角函数概念、图象和性质,诱导公式,同角关系式,两角和与差的三角公式等密切相关

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目