题目内容
如果θ是第二象限角，那么
是（ ）
| θ |
| 2 |
分析：由θ的范围判断θ的一半的范围，先写出角的范围，再除以2，求出角的一半的范围，看出角的范围．
解答：解：∵θ是第二象限角，
∴θ∈（2kπ+
，2kπ+π），k∈Z，
∴
∈（kπ+
，kπ+
），k∈Z．
∴
是第一或三象限角．
故选：B．
∴θ∈（2kπ+
| π |
| 2 |
∴
| θ |
| 2 |
| π |
| 4 |
| π |
| 2 |
∴
| θ |
| 2 |
故选：B．
点评：本题考查了角的范围，考查象限角，解题的关键是写出象限角的范围，根据不等式的做法，写出要求的角的范围．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
如果θ是第二象限角，且满足cos
-sin
=
，那么
（ ）
| θ |
| 2 |
| θ |
| 2 |
| 1-sinθ |
| θ |
| 2 |
| A、是第一象限角 |
| B、是第三象限角 |
| C、可能是第一象限角，也可能是第三象限角 |
| D、是第二象限角 |
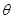是第二象限角,且
,那么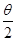
所在象限为第几象限