Question

（本小题满分12分）

抛物线顶点在坐标原点，焦点与椭圆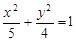的右焦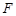点重合，过点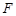斜率为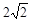的直线与抛物线交于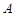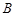，两点.

（Ⅰ）求抛物线的方程；

（Ⅱ）求△的面积．

 

Answer 1

【答案】

(1)  (2)

【解析】

试题分析：解：（Ⅰ）由题意可知，椭圆的右焦点，故抛物线焦点，

所以抛物线的方程为.                                  …………………4分

（Ⅱ）直线的方程为，设，

联立，消去，得，             ………………………6分

，，

因为                           …………………9分

由                        ………………………11分

所以                                           ………………………12分

考点：本试题考查了抛物线的方程运用。

点评：解决该试题的关键是利用椭圆的焦点坐标来求解抛物线方程，进而得到结论，同时能联立方程组，进而得到相交弦的端点坐标关系式，结合面积公式来求解，属于中档题。