题目内容
设函数 .
.
(1)当 ,
, 时,求所有使
时,求所有使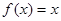 成立的
成立的 的值。
的值。
(2)若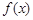 为奇函数,求证:
为奇函数,求证:  ;
;
(3)设常数 <
< ,且对任意x
,且对任意x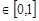 ,
,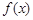 <0恒成立,求实数
<0恒成立,求实数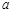 的取值范围.
的取值范围.
【答案】
解:(1)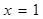 或
或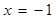 ;(2)见解析 ;(3)
;(2)见解析 ;(3)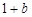 <
<
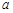 <
<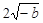 .
.
【解析】本试题主要是考查了函数的奇偶性与函数与不等式关系的运用,以及函数解析式的综合运用。
(1)当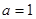 ,
,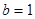 时,函数
时,函数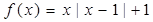 .
.
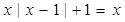
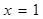 或
或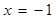
(2)若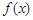 为奇函数,则对任意的
为奇函数,则对任意的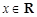 都有
都有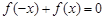 恒成立,则展开可得。
恒成立,则展开可得。
(3)由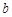 <
<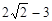 <0, 当x=0时
<0, 当x=0时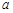 取任意实数不等式恒成立.
取任意实数不等式恒成立.
当0<x≤1时,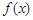 <0恒成立,也即
<0恒成立,也即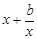 <
<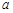 <
<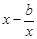 恒成立.
恒成立.
从而构造函数得到结论。
解:(1)当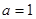 ,
,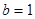 时,函数
时,函数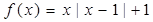 .
.
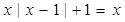
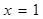 或
或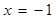
(2) 若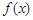 为奇函数,则对任意的
为奇函数,则对任意的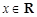 都有
都有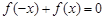 恒成立,
恒成立,
即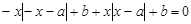 ,
,
令x=0得b=0,令x=a得a=0,∴
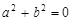
(3)由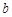 <
<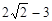 <0, 当x=0时
<0, 当x=0时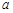 取任意实数不等式恒成立.
取任意实数不等式恒成立.
当0<x≤1时,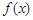 <0恒成立,也即
<0恒成立,也即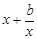 <
<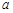 <
<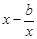 恒成立.
恒成立.
令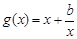 在0<x≤1上单调递增,∴
在0<x≤1上单调递增,∴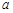 >
>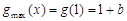 .
.
令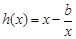 ,则
,则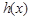 在
在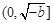 上单调递减,
上单调递减,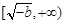 单调递增
单调递增
 当
当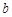 <
<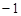 时,
时,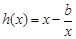 在0<x≤1上单调递减;
在0<x≤1上单调递减;
∴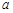 <
<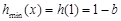 ,∴
,∴
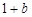 <
<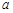 <
<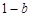 .
.
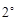 当
当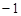 ≤
≤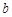 <
<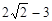 时
时 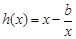 ≥
≥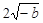 .
.
∴ 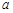 <
<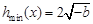 .∴
.∴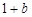 <
<
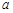 <
<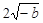 .
.

练习册系列答案
相关题目
 .
. .
. 。
。 的极值;
的极值; 2时,讨论函数
2时,讨论函数 成立,求
成立,求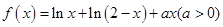 。
。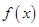 的单调区间。
的单调区间。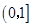 上的最大值为
上的最大值为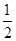 ,求a的值。
,求a的值。