题目内容
一个三棱锥的顶点在空间直角坐标系O-xyz中的坐标分别是(1,-2,-3),(0,1,0),(0,1,1),(0,0,1),则该四面体的体积为( )
分析:通过点A、B、C、D的坐标,求出底面ABC的面积,高的数值,然后求出三棱锥A-BCD的体积.
解答:解:设A(1,-2,-3),B(0,1,0),C(0,1,1),D(0,0,1),
则B、C、D三点在平面xoz内,
=(0,0,1),
=(0,1,0),
∵
•
=0,
∴BC⊥DC
底面三角形BCD为直角三角形,且|BC|=|DC|=1,
其面积S=
×1×1=
;三棱锥的高为1,
∵A的横坐标为1,∴A到平面xoz的距离为1,
∴三棱锥的体积V=
×
×1=
.
故选D.
则B、C、D三点在平面xoz内,
| BC |
| DC |
∵
| BC |
| DC |
∴BC⊥DC
底面三角形BCD为直角三角形,且|BC|=|DC|=1,
其面积S=
| 1 |
| 2 |
| 1 |
| 2 |
∵A的横坐标为1,∴A到平面xoz的距离为1,
∴三棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
故选D.
点评:考查空间直角坐标系,点的坐标的理解,通过转化思想求出底面面积是解题的关键,考查计算能力.

练习册系列答案
相关题目
 的顶点
的顶点 在平面
在平面 上的射影是
上的射影是 ,给出以下命题:
,给出以下命题: ,
, ,则
,则 的垂心
的垂心 两两互相垂直,则
两两互相垂直,则 ,
, 的中点,则
的中点,则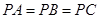
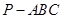 的顶点
的顶点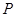 在底面
在底面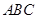 内射影
内射影 在
在 内部,且到三个侧
内部,且到三个侧