题目内容
设集合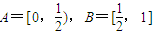 ,函数
,函数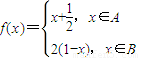 ,若x∈A,且f[f(x)]∈A,则
,若x∈A,且f[f(x)]∈A,则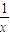 的取值范围是 .
的取值范围是 .
【答案】分析:先求出f(x),然后按f(x)∈A,f(x)∈B两种情况进行讨论求出f[f(x)],再根据f[f(x)]∈A可得x的范围,进而求得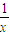 的取值范围.
的取值范围.
解答:解:因为x∈A,所以f(x)=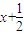 ,
,
(1)当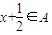 ,即-
,即- ≤x<0时,f[f(x)]=f(
≤x<0时,f[f(x)]=f(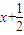 )=x+1,
)=x+1,
又f[f(x)]∈A,所以0≤x+1< ,解得-1≤x<-
,解得-1≤x<- ,此时无解;
,此时无解;
(2)当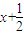 ∈B,即0≤x
∈B,即0≤x 时,f[f(x)]=f(
时,f[f(x)]=f(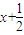 )=2[1-(
)=2[1-( )]=1-2x,
)]=1-2x,
又f[f(x)]∈A,所以0≤1-2x< ,解得
,解得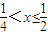 ,
,
故2≤ <4,
<4,
故答案为:[2,4).
点评:本题考查分段函数的求值,考查分类讨论思想,考查学生的运算能力,属中档题.
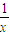 的取值范围.
的取值范围.解答:解:因为x∈A,所以f(x)=
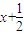 ,
,(1)当
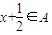 ,即-
,即- ≤x<0时,f[f(x)]=f(
≤x<0时,f[f(x)]=f(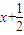 )=x+1,
)=x+1,又f[f(x)]∈A,所以0≤x+1<
 ,解得-1≤x<-
,解得-1≤x<- ,此时无解;
,此时无解;(2)当
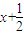 ∈B,即0≤x
∈B,即0≤x 时,f[f(x)]=f(
时,f[f(x)]=f(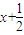 )=2[1-(
)=2[1-( )]=1-2x,
)]=1-2x,又f[f(x)]∈A,所以0≤1-2x<
 ,解得
,解得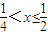 ,
,故2≤
 <4,
<4,故答案为:[2,4).
点评:本题考查分段函数的求值,考查分类讨论思想,考查学生的运算能力,属中档题.

练习册系列答案
相关题目